Noções e Proposições primitivas
1. Noções Primitivas
A Geometria Plana estuda os pontos e os conjuntos de pontos (reta, semi-reta, segmento, plano, círculo, circunferência e/ou as figuras geométricas planas).
A linguagem LÓGICA é usada nos textos matemáticos, assim ocorre o emprego contínuo de conceitos que por sua vez, os consideramos conhecidos depois que são definidos e as suas propriedades são consideradas verdadeiras depois que demonstradas. Todavia, se faz necessário estabelecer um início conceitual, no qual se constrói todo o conhecimento da Geometria Plana. Logo, adotamos alguns conceitos sem definição, ou seja, os CONCEITOS PRIMITIVOS, onde todos os outros, a partir deles, são definidos. Isso é necessário para que essa teoria tenha uma finalidade prática, onde pela simplicidade dos conceitos primitivos, todas as pessoas possam ter o mesmo significado, sem que façam definição. O PONTO é um conceito fundamental da Geometria Plana, de onde todos os demais entes se derivam, ou seja: a reta, a semi-reta, o segmento, o plano. o círculo, a circunferência e/ou as figuras geométricas planas. Você já imaginou um ponto? Como é um ponto? Podemos fazer um Ponto? Na realidade, nós construímos representações de ponto ou de um ponto. Observe:
1. O átomo e as suas partículas
2. Os grãos de areia

3. As estrelas, numa noite estrelada

4. Uma bolinha preta numa folha de papel

RETA e PLANO são dois CONCEITOS PRIMITIVOS que são fundamentais na Geometria. A ideia de uma reta pode ser sugerida por um fio esticado e a ideia de plano, pela tela de um celular, tela de uma TV ou, ainda, a superfície ou o tampo de uma mesa. Porém, o fio esticado terá COMEÇO e FIM e a mesa suas beiradas, e, ambos, têm a sua espessura. Lembrando que, para materializarmos as ideias de reta e plano, seriam necessárias coisas/objetos sem espessura e que se estendessem infinitamente. É lógico, que só podemos imaginar a existência dessas coisas. Então, concluímos:
RETA E PLANO SÃO CONCEITOS PRIMITIVOS!1. Uma reta, estrada.

2. Um fio de primo

3. Você consegue ver representação de retas, na imagem abaixo?
4. O tampo da mesa. Uma representação de um plano.

Reta "r"
Plano alfa
Usualmente, são adotados como representações gráficas de reta e plano os desenhos abaixo:
Retas "s" e "t"
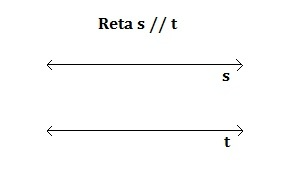
Plano alfa
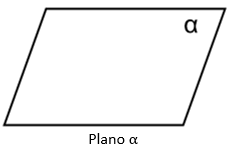
Deve-se imaginar que a linha das retas "s" e "t" se prolongam em ambos os sentidos, como sugerem as setas e que a figura de baixo mostra penas uma parte/porção/pedaço do plano, o qual, na realidade, não tem esse contorno. As retas são indicadas por letras latinas minúsculas (a, b, c, ...) e os planos, por letras gregas minúsculas (, , ,...).
2. Proposições Primitivas
As proposições (propriedades, afirmações) geométricas são aceitas mediante demonstrações. As proposições primitivas ou postulados ou axiomas são aceitos sem demonstração. Iniciaremos a Geometria Plana com alguns postulados relacionando o ponto, a reta e o plano.
Posições de dois pontos e de ponto e reta
Pontos colineares (alinhados), não colineares (não alinhados) e coplanares
Dois ou mais pontos são colineares se todos eles pertencem a uma mesma reta. Dizemos, também, que esses pontos estão alinhados. Caso contrário, eles são não colineares ou estão não alinhados. Pontos coplanares são pontos que pertencem ou estão num mesmo plano.
Três pontos não colineares determinam um único plano que passa por eles. Podemos dizer, também, que: dados três pontos A, B e C não colineares, existe um único plano tal que A e B e C . Existem, ainda, as seguintes formas: Três pontos não alinhados determinam completamente um plano, ao qual eles pertencem e, outra forma é: por três pontos não colineares passa um único plano. Simbolicamente, representamos por:
A, B, C não alinhados (A e B e C )O plano determinado pelos pontos A, B e C pode ser indicado por pl (ABC), ou pl (ACB), ou pl (BCA), etc, indiferentemente. Quando apoiamos no chão um tripé, observamos que o aparelho obtém uma posição estável, mesmo se o terreno for irregular. O contrário ocorreria se fosse uma mesa ou cadeira com quatro pés, pois há a possibilidade de não ter estabilidade (mancar). Num piso bem plano, três pés da mesa ou da cadeira vão ficar apoiados: o quarto pé poderá ou não pertencer ao plano determinado, pelos outros três. Desta forma, tem-se uma materialização da ideia de plano deste postulado.

Plano em 3D, no Geogebra
Se uma reta tem dois pontos distintos num plano, então a reta está contida nesse plano. Outra forma de anunciar esse postulado é: se dois pontos distintos A e B de uma reta r pertencem a um plano , então todos pontos dessa reta pertencem a .
![[size=85]Se encostarmos dois pontos A e B de uma régua sobre a superfície da mesa, todos os pontos da régua ficarão encostados na mesa.[/size]](https://beta.geogebra.org/resource/ajxkwjhp/AtKCvXSqpHHFIZjH/material-ajxkwjhp.png)
Simbolicamente, escrevemos: (A B, A , B ) r . Vale salientar que a reta r é um conjunto de pontos, logo é um subconjunto do plano .
Usando o postulado da existência, tomemos uma reta r, um ponto P em r (P r) e um ponto Q fora de r (Q r). Os pontos P e Q são distintos, pois um deles pertence a r e o outro não. Usando o postulado da determinação, considerando a reta s determinada pelos pontos P e Q. As retas r e s são distintas, pois se coincidissem o ponto Q estaria em r (e ele foi construído fora de r), e o ponto P pertence às duas. Logo, r e s são concorrentes.