Collatz után szabadon (8.)
- Szerző:
- Tarcsay Tamás
- Témák:
- Sorozatok és sorok
Ennek az anyagnak a végén egy sejtés van. Aki ellenpéldát talál, feltétlenül jelezze!
Vizsgáljuk a következő rekurzióval adott sorozatokat!
, ha an páros
an+1=3an+1, ha an páratlan
A következő aplettel vizsgálhatók a sorozatok különböző első tagok esetében.
Az auto feliratú csúszka megmozdításakor a sorozat tagjainak megjelenítése a "T"-re való kattintás nélkül is történik. Ennek sebességét a v csúszkával változtathatjuk.
(Megjegyzés a technikai részletek iránt érdeklődőknek:
Ez a GeoGebra eszközeivel nem könnyen valósítható meg. Dr. Szilassi Lajos tanár úrnak köszönhetően ez megoldható. Erről itt olvashatunk.)
A tapasztalat az, hogy bármely pozitív egész számot választjuk a sorozat első tagjának, mindegyik sorozatnak tagja az 1.
Ezt a sejtést Lothar Collatz fogalmazta meg 1937-ben. A sejtést azóta sem sikerült bizonyítani.
Az érdekes az, hogy egy nagyon egyszerű eszközökkel megfogalmazott sejtés, a bizonyítása nagyon nehéz.
Megjegyezzük, hogy a Collatz-sorozattal egy másik anyagban más szempontból foglalkoztunk.
Szórakoztató játék lehet más - hasonló - rekurziókkal definiált sorozatok vizsgálata. Az alábbi GeoGebra aplettel olyan sorozatok vizsgálhatók amelyek rekurziója páros esetre egyezik a Collatz-féle definícióval.
Ha a definíciót így változtatjuk:
an+1=3an-1, ha an páratlan,
akkor az alábbi gráf mutatja, hogy melyik számot melyik szám követi a sorozatban,
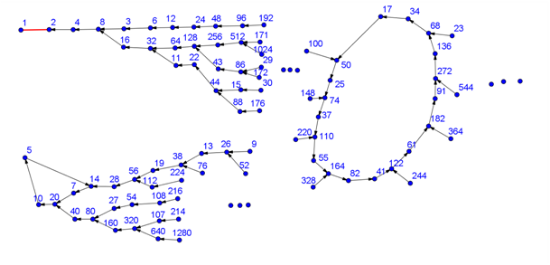
Sejtés
Ha a definíciót így változtatjuk:
an+1=3an+3, ha an páratlan,
akkor úgy tűnik, hogy bármely első tag esetén a sorozatnak tagja a 3.