The Great Adirondack Surveyor
Have you ever driven past a construction site and spotted a crew working with a fancy tripod? Well you observed a surveyor in the field taking measurements and marking where something is, should, or will be.
Surveying is an important part of all forms of construction as it allows you to place objects exactly where they were planned to go. You don't want to start building a bridge, and get to the other side and find it's just a few feet off.
Using a form of math called Triangulation, given just an angle, and the length of one side of a triangle, then all other information of that triangle can found.
In modern day's, they use a machine called a totaling station that looks for specific GPS coordinates and sends a laser to a reflector. That distance between the station and reflector becomes your known side length. The tricky part is finding the angle between the reflector, total station, and your third point.
Finding the angle between the 3 points is easier today because the machine calculates it for you. Before computers and calculators, all of the Trigonometry was preformed by hand, in the field.
The common items used in rugged terrain were as follows: Flares, Reflectors, Telescopes, Ax's, Saws, Fire, Boats, Chains, Plum Bobs, Levels, and many more.
While today we have the luxury of knowing the elevation of where we stand with GPS, back in the 1870's it was a different story.
Over in New York state, in what would become the Adirondack Park. One man's vision to preserve 6 million acres of forest began with a book. As an author himself, Verplank Colvin accepted a copy of a book written by his colleague Alfred Billings Street, who he'd later thank by naming a mountain after him. This book led Colvin to a vacation in the wood's of the north country where soon he would find his destiny.

Verplank Colvin
Colvin set off on a few hikes and explorations over the next three years, falling in love with the immense natural beauty of the Adirondack Mountains. On one fateful day he summited Mount Marcy, the tallest mountain in all of New York. He asked himself one question that would end up shaping the Adirondacks forever.
How tall is it?
Pythagorean Theorem Vs Law of Cosines
Before you continue with this lesson, please visit https://www.geogebra.org/m/dwqcqcxq This demonstration of the Pythagorean Theorem and Law of Cosines is best accompanied with this lesson from Greg.P.

Colvin was enthralled with this question. Quite conveniently the state of New York was looking for someone to survey this massive swath of rugged mountainous terrain.
So when Colvin wrote to his government, they responded with a crew of 100 men, $1,000 dollars, some chains, boats, flares, camping supplies, and a desire to discover the unknown.
Up until this point, no maps existed of the Adirondack mountains. Since the technology of the time required a great deal of physical labor just to place a third point, triangulation was a difficult task.
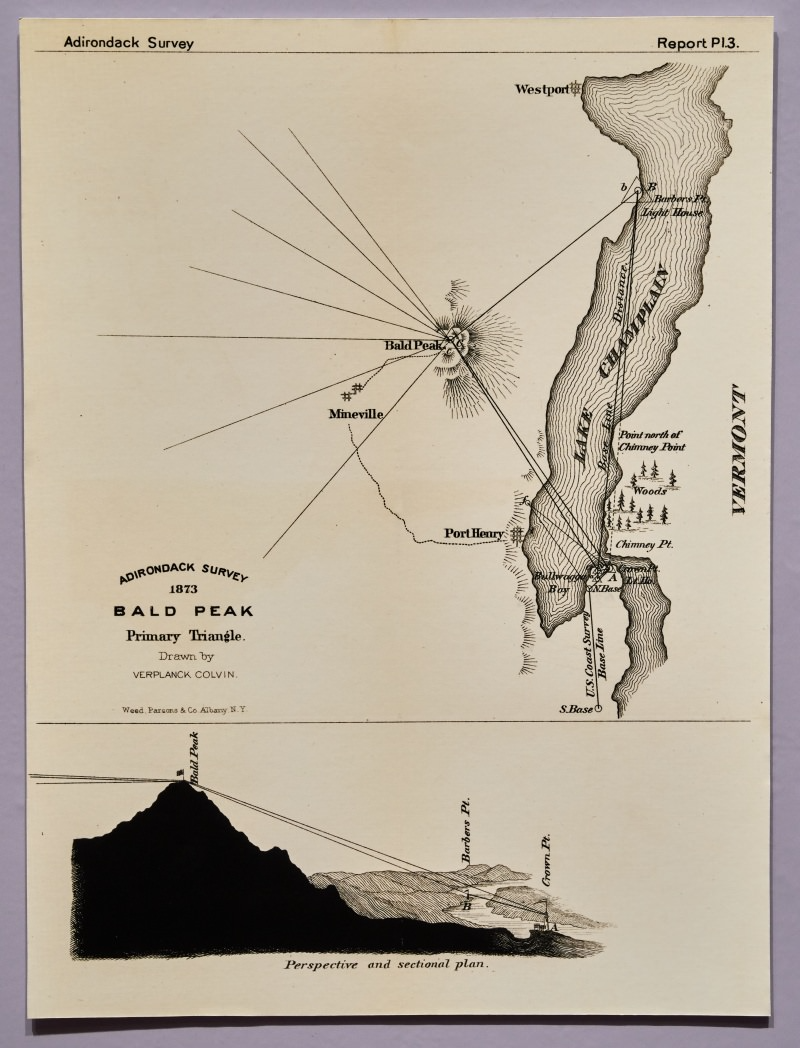
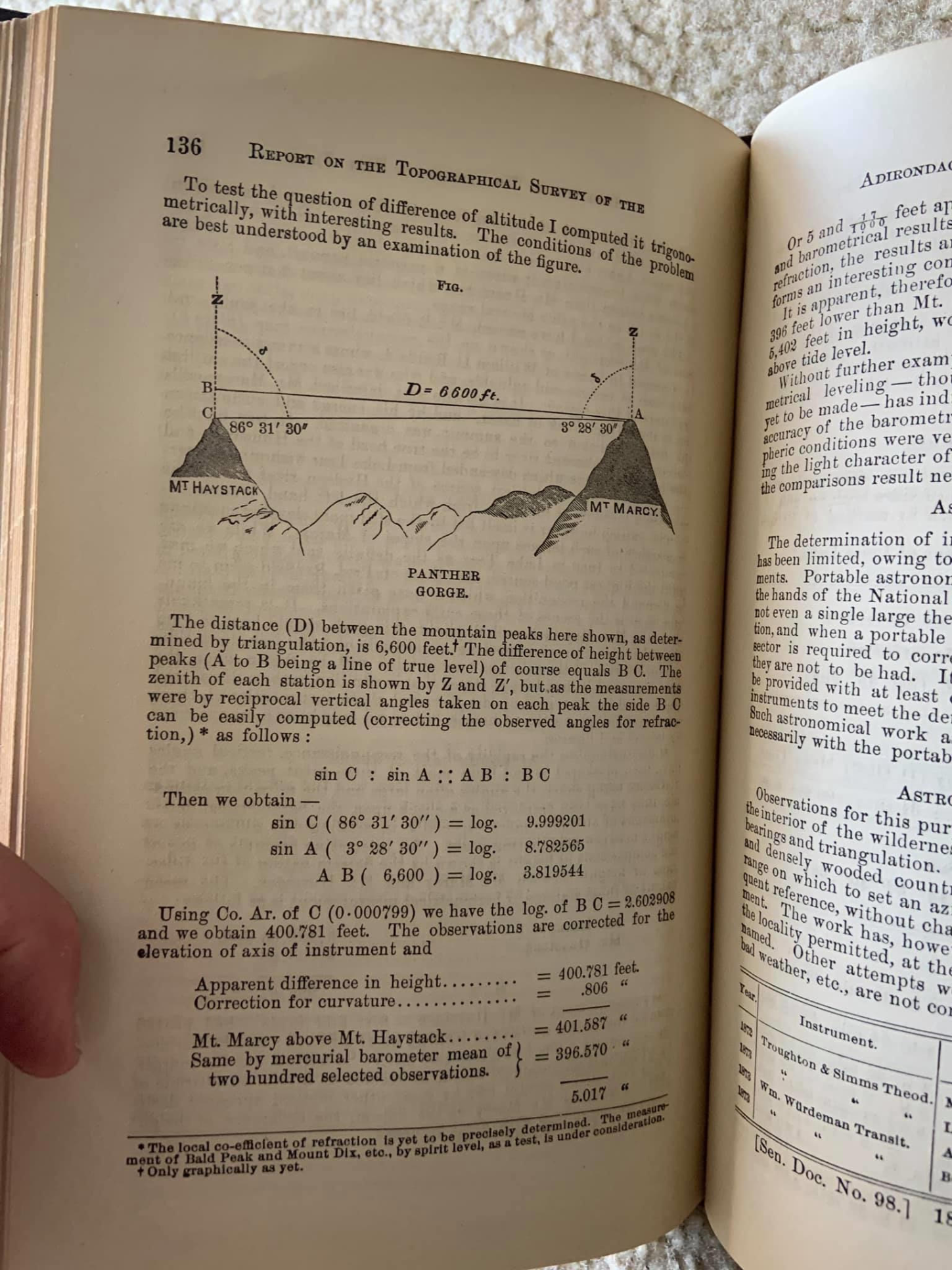
The image above is a page from Colvin's Adirondack Survey reports, you can observe the primary triangle used to calculate the summit height of Bald Peak from lake Champlain.
Reflector Tower

Methods
While the reflector towers, flares, and other devices were used to set the points a triangle would be formed from, the process of finding the actual length of that distance was tricky.
Due to uneven, and rugged terrain, measurements were slow. Chunks at a time, of smaller triangles that would eventually yield a line, of which an angle could be calculated from the end of your measure. Often the end of measure was a lake, benchmark, or summit. Chains called furlongs would be used to keep track of the distance covered between measurements. Colvin had 111 benchmarks, but took over 800 measurements across his 40 mile trek.


Referencing the page above from Colvin's own survey report, he would point his scope at a peak, and wait until the level on the scope was well, level. Then ascending up the slope, he would take a new barometer measurement to determine the height change. This would serve as one leg of the triangle. From that point he would again aim his scope at the previous known reference peak, and note the change in degrees on the level. This would end up yielding the degree of the angle necessary to calculate the entirety of the triangle.
Doing this he would keep angular sight lines as reference gradients that converged at a benchmark.
Benchmarks would be constructed when previous ones no longer remained visible from an elevated point of measure. An example of which being, a smaller mountain is now blocking the view.
Triangle Forming Exercise
Using the lines drawn by Verplank Colvin, move the interactive demonstration of the Law of Cosines to visualize the method's of his achivement.
Finding Marcy!!!
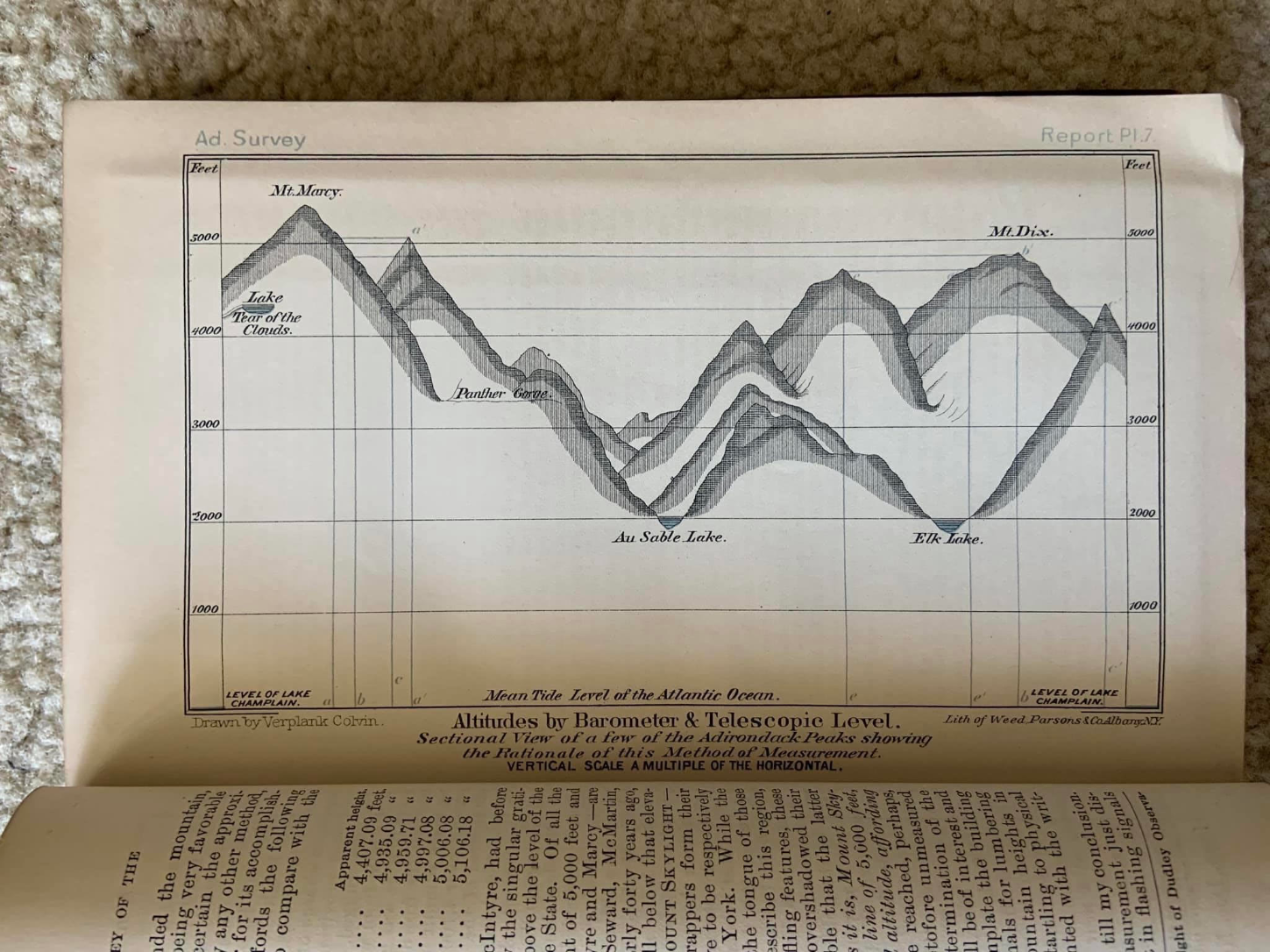
Mt Marcy was the goal of Colvin's expedition after all. So it would only make sense that he would treasure the moment for the rest of his life. The final calculations and drawing of which would later become the leather mark indented in the cover of his reports. The numerical calculations still stand as a feat of their times for such accuracy, but it was the conditions in which he endured that made the measurement all the more memorable.
Faced with a late October snowstorm, the decision to push towards the summit of Marcy had the risk of stranding the crew in Panther Gorge for the winter, which would have ended in their demise. With just feet to go, Colvin pushed forth, not letting his effort go in vain.
A detailed account of his harrowing actions and inventions can be found at the Adirondack Museum in Blue Mt Lake, while copies of his reports never left his private collection, due to Governor of New York, Theodore Roosevelt firing him to create the new position of state engineer.
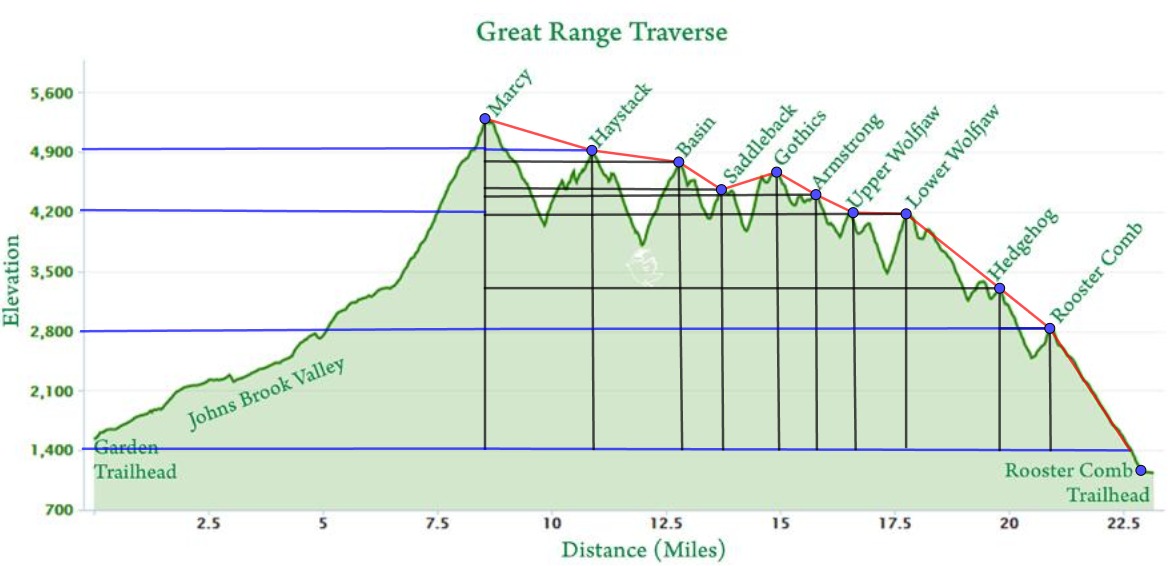
Move the points labeled Marcy & Lower WolfJaw to their respective summits
Final Calculations
Law Of Cosines
Where the Pythagorean theorem relies on the use of right Triangles, the Law of Cosines can be used for other triangles.

Conclusion
Verplank Colvin showed that mathematics can be used in the most extreme of environments. With regard to the concepts that will be covered later on, everything has a practical application.