The Solutions to Linear Systems
Back in Algebra 1 you were taught that a linear equation in two variables could be represented graphically as a line of points in the plane. Thus the solution set to a system of two or more linear equations in two variables could take three possible forms:
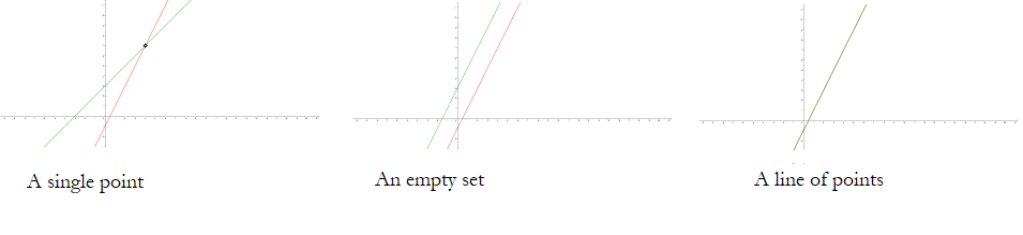
A linear equation in three variables can similarly can be represented graphically as a flat plane of points in . ( is a name we give to a 3-d coordinate system. The symbol stands for the set of real numbers and the number 3 tells you how many axes to use. With this naming scheme, the plane is called .)
Move the sliders in the applet below to see the effect on the corresponding plane.
Take some notes about your observations from the preceding applet.
Just like in , the solution set to a system of linear equations in three variables can be represented graphically as the common intersection of several planes. In the applet below you can change the coefficients in three different linear equations in three variables and view the intersection of the corresponding planes.
When examining a linear system with three unknowns, there are four possible types of solution sets. Describe each possible solution set.