Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Transformations (Translation, Reflection & Rotation)

Author:Jainesh Patel

Translation

In this section, students will be able to describe the effect of translations on two dimensional figures using coordinates. Note: The brown triangle is our pre-image/the original image meaning we are starting with that image. The red triangle is our new image after the transformation (in this case translation) has been performed. We denote our new image using prime notation (single quotation mark, ex. A'). Before answering any questions, play around with the translation sliders. Blue slider translates the figure vertically and the red slider translates the figure horizontally. Pay attention to coordinate changes while interacting with the sliders below.

Translation

Question 1

Which term best describes a translation?

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Question 2

Translate the original triangle ABC 3 units to the left and 2 units up. What are the new coordinate points of Triangle A'B'C'? Hint: Make sure the triangles are exactly on top of each other before performing the translation.

Question 3

Translate the original triangle ABC 3 units to the left and 2 units up. What are the new coordinate points of Triangle A'B'C'? Hint: Make sure the triangles are exactly on top of each other before performing the translation.

Question 4

What happens to x coordinate value when you translate the figure to the left? What about when you translate the figure to the right?

Question 5

What happens to y coordinate value when you translate the figure down? What about when you translate the figure up?

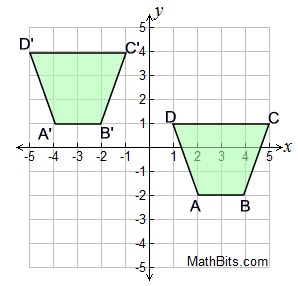
Question 6

For the given figures ABCD and A'B'C'D', Describe how the pre-image is translated to the new image? Are the two figures congruent?

Reflection

In this section, students will be able to describe the effect of reflections on two dimensional figures using coordinates. For the reflection transformation, we will focus on two different line of reflections. Reflection over x-axis and y-axis. Below you are provided with three figures. The original pre-image (brown) and reflection over the y-axis (red) and over the x-axis (blue). Discover how figures are reflected over the x and y-axis by playing around with the original figure. Reshape the figure, move the figure around to learn. Have fun! Also think about mirrors, since we are going to work with coordinate points, what do you think will happen to the points when you reflect? Hint: Think about mirror, what happens when you raise your left arm, what do you see happening in a mirror?

Reflection

Question 1

Which term best describes a reflection?

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Question 2

Rearrange the triangle so point A is at (4, 2). What is the point of reflection over the y-axis for point A? Now translate point A, 2 units up. What is the new point of reflection for over the y-axis for point A?

Question 3

Relating to question 1, what difference do you notice about the coordinate points before and after the reflection over the y-axis?

Question 4

Rearrange the triangle so point B is at (5, 1). What is the point of reflection over the x-axis for point B? Now translate point B, 3 units to the right. What is the new point of reflection for over the y-axis for point B?

Question 5

Relating to question 3, what difference do you notice about the coordinate points before and after the reflection over the x-axis?

Question 6

Which formula below best illustrates a reflection over the y-axis?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 7

Which formula below best illustrates a reflection over the x-axis?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 8

Reflect the points below over the x-axis. What the new coordinate points A', B' and C'? A (1, 3) B (3, 4) C (-2, 5)

Question 9

Reflect the points below over the y-axis. What the new coordinate points A', B' and C'? A (5, 2) B (1, 6) C (3, -7)

Question 10

A reflection over the x-axis makes the ________ opposite.

Select all that apply
  • A
  • B
Check my answer (3)

Question 11

A reflection over the y-axis makes the ________ opposite.

Select all that apply
  • A
  • B
Check my answer (3)

Rotation

In this section, students will be able to describe the effect of rotations on two dimensional figures using coordinates. For the rotation transformation, we will focus on two rotations. We will rotate our original figures 90 degrees clockwise (red figure) and 180 degrees (blue figure) about the origin (point O). Spend some time to play around with the original figure and see if you can notice the pattern with the change in coordinate points for the new figures of 90 and 180 degree rotations. Feel free to try different degrees for rotation, change it to counterclockwise to see how the figures and coordinates change. Have fun!

Rotation

Question 1

Which term best describes a rotation?

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Question 2

A copy of a figure is called ________.

Select all that apply
  • A
  • B
Check my answer (3)

Question 3

Rigid transformations (translation, reflection, rotation) produce __________ figures.

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Question 4

Rearrange the triangle so point A is at (5, 7), point B is at (9, 6) and point C is at (4, 3). What are the new coordinate points of A', B' and C' after a 90 degree clockwise rotation? What pattern you notice between the original points and the rotated points?

Question 5

Rearrange the triangle so point A is at (5, 7), point B is at (9, 6) and point C is at (4, 3). What are the new coordinate points of A', B' and C' after a 180 degree rotation? What pattern you notice between the original points and the rotated points?

Question 6

To rotate a figure 90 degrees clockwise, use this representation:

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Question 7

To rotate a figure 180 degrees, use this representation:

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 8

Rotate the points below 90 degrees clockwise about the origin. What the new coordinate points A', B' and C'? A (4, 4) B (2, -1) C (-2, 3)

Question 9

Rotate the points below 180 degrees about the origin. What the new coordinate points A', B' and C'? A (-2, 3) B (4, -1) C (-5, -2)

New Resources

Discover Resources

Discover Topics