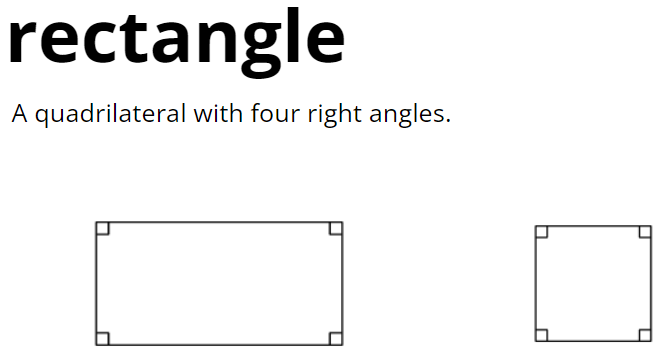
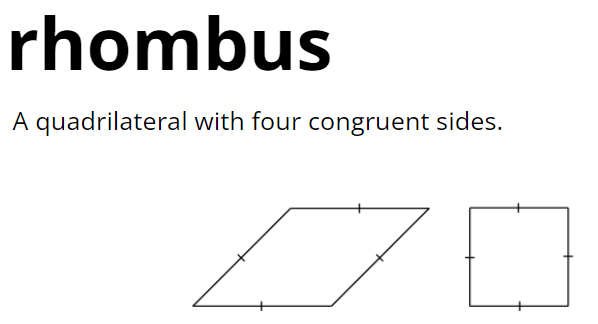
L2.12 - Proofs about Quadrilaterals
Learning Intentions and Success Criteria
- Comprehend a conjecture and express it (in writing) as a specific statement to prove.
- Critique others' reasoning (in spoken and written language) about quadrilaterals.
- Prove (in writing) theorems about quadrilaterals.
- Critique a proof about quadrilaterals.
- Prove theorems about quadrilaterals.
- Rewrite a conjecture so it is specific enough to prove.
12.1: Play with Parallelograms
1. Which figures (if any) are always rectangles? Which figures can be dragged to make a rectangle?
2. Which figures (if any) are always parallelograms? Which figures can be dragged to make a parallelogram?
Six Properties of Parallelograms
- Opposite sides are congruent (AB CD).
- Opposite angles are congruent (D B).
- Consecutive angles are supplementary (mA + mD = 180°).
- If one angle is right, then all angles are right.
- The diagonals of a parallelogram bisect each other.
- Each diagonal of a parallelogram separates it into two congruent triangles.
Show Properties 1 (Opposite sides are congruent) & 2 (Opposite angles are congruent) of Parallelograms.
Write an explanation in detail for property 1 of parallelograms.
1. Opposite sides are congruent.
Write an explanation in detail for property 2 of parallelograms.
2. Opposite angles are congruent.
Show Property 3 of Parallelograms (Consecutive angles are supplementary).
Write an explanation in detail for property 3 of parallelograms.
3. Consecutive angles are supplementary.
Show Property 4 of Parallelograms (If one angle is right, then all angles are right).
Write an explanation in detail for property 4 of parallelograms.
4. If one angle is right, then all angles are right.
Show Property 5 of Parallelograms (The diagonals of a parallelogram bisect each other).
Write an explanation in detail for property 5 of parallelograms.
5. The diagonals of a parallelogram bisect each other.
Show Property 6 of Parallelograms (Each diagonal of a parallelogram separates it into two congruent triangles).
Write an explanation in detail for property 6 of parallelograms.
6. Each diagonal of a parallelogram separates it into two congruent triangles.
Review Rigid Transformations
Write a sequence of rigid motions to take figure ABC to figure DEF.

Learning Intentions and Success Criteria
- Comprehend a conjecture and express it (in writing) as a specific statement to prove.
- Critique others' reasoning (in spoken and written language) about quadrilaterals.
- Prove (in writing) theorems about quadrilaterals.
- Critique a proof about quadrilaterals.
- Prove theorems about quadrilaterals.
- Rewrite a conjecture so it is specific enough to prove.
Cool-Down: A Proof In Time Saves Nine
Elena wants to prove that a quadrilateral with 4 right angles must have congruent opposite sides. Explain to Elena how she can use the fact that all rectangles are parallelograms in her proof.
GLOSSARY