het Parthenon in cijfers en het Griekse wiskundige denken
het Parthenon in cijfers
Een uitstekende referentie is 'The Parthenon's Main Design Proportion and Its Meaning', de vaak geciteerde doctoraatsproefschrift van Anne Bulckens over de verhoudingen van het Parthenon (447 - 437 v.Chr.).
Een samenvatting van de bevindingen vind je o.a. in een artikel van Jay Kappraf.
Anne Bulckens’ Analysis of the Proportions of the Parthenon and its Meanings - Jay Kappraf
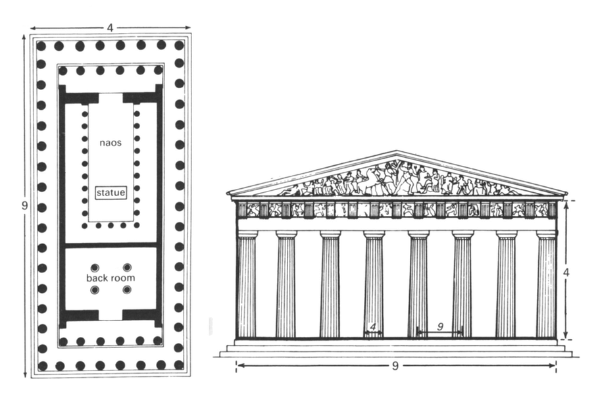
Net zoals anderen voor haar vindt Anne Bulckens in het Parthenon de verhouding 9 : 4 terug, zowel in de afmetingen van het grondplan als in die van de gevelopstand.
De 9 : 4 rechthoek wordt niet getekend op een foto, maar een tekening op basis van opmetingen.
- De horizontale afstand is de breedte van het stylobaat.
- De verticale afmeting is de hoogte van de kolommen plus de entablatuur of hoofdgestel.
Versleep de beide rode punten en probeer een gulden rechthoek in te passen in de gevel van het Parthenon
een module voor het Parthenon
Naast de buitenafmetingen van het Parthenon onderzocht Anne Bulckens of ze ook een onderliggend schema van verhoudingen kon terugvinden.
Ze ontdekt een enkele module van 857.6 mm, de gemiddelde breedte van een ‘theoretische triglief’. Dit komt overeen met wat Vitrivius 4 eeuwen later schreef in zijn de Architectura, de enige verhandeling van die omvang uit de Klassieke Oudheid die bewaard is gebleven.
Deel je deze module door 2.5 dan krijg je een ‘Parthenonvoet’. Verdeel je die in 16 gelijke delen, dan krijg je een zgn. dactylys (D). Het mooie nu is dat alle afmetingen van het Parthenon kunnen uitgedrukt worden in gehele veelvouden van deze dactylus.
Zo zie je in bovenstaande tekening de gevelafmetingen uitgedrukt in dactyli (D).
verhoudingen in het Parthenon
Anne Bulckens vestigt ook de aandacht op de wiskunde en numerologie van Pythagoras. De verhouding 9 : 4 is dan wel de meest zichtbare verhouding, maar misschien is de fundamentele verhouding van het gebouw wel 3 : 2 en is 6 (het meetkundig gemiddelde van 9 en 4) essentieel.
Je krijgt dan immers de middelevenredigheid 9 : 6 :: 6 : 4 en de verhouding 3 : 2, de kwintverhouding waarop Pythagoras zijn toonladder opbouwde (zie Pythagoras voor meer informatie over toonladders en stemmingen).
Meer details over hoe je deze verhoudingen terugvindt in het Parthenon kan je lezen in het artikel van Jay Kapraff, dat je kan openen hoger in deze pagina.
cijfers en verhoudingen in het Pythagorese denken
Ons lijkt die 9 : 6 :: 6 4 verhouding vergezocht. Wij kijken naar de dingen en zoeken wetmatigheden of meten afstanden. De pyhtagoreeërs redeneren echter omgekeerd. In hun zijnsleer vormen getallen en hun verhoudingen net de kern der dingen. Meetkunde en muziek zijn hierbij slechts de zichtbare en hoorbare uitingen van deze verhoudingen. Zo wordt bv. het getal 10 voorgesteld als een driehoeksgetal. Het heeft de vorm van een viertal (tetraktys).

Het getal10, een hogere vorm voor de eenheid, is in deze vorm de combinatie van de eerste vier getallen en symbool voor de opbouw van de kosmos.
1 vormt de basis voor een punt, 2 voor een lijn, 3 voor een plat vlak en 4 voor de ruimte.
Tegelijk stemmen de onderlinge verhoudingen overeen met de frequentieverhoudingen van de harmonische samenklanken in de muziek:
- octaaf 1 : 2
- kwint 2 : 3
- kwart 3 : 4
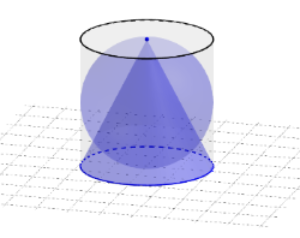
![De doorsnede van twee loodrecht op elkaar geplaatste cilinders, ingeschreven in een kubus, is het zogenaamde [url=https://nl.wikipedia.org/wiki/Steinmetzlichaam#:~:text=Een%20Steinmetzlichaam%20is%20de%20doorsnede,elkaar%20onder%20een%20rechte%20hoek.]Steinmetzlichaam[/url].
Archimedes vergeleek de inhoud van dit lichaam met de inhoud van de kubus en vond (weer) de verhouding 2 : 3.](https://beta.geogebra.org/resource/dzgcyr8n/ATE66QwCcO5LuwPp/material-dzgcyr8n.png)
een kleine tijdlijn
Hét Griekse denken bestaat niet. Ook in het Antieke Griekenland zijn wiskunde en filosofie geen monolithische blokken.
- In het Pythagorese denken staan verhoudingen van gehele getallen centraal. Men rekende ook enkel met gehele getallen en verhoudingen ervan. Waar wij kennen als de lengte van de diagonaal van een vierkant met zijde 1, vormde voor de Grieken die diagonaal de zijde van een vierkant met een oppervlakte die dubbel zo groot is als het vierkant met zijde 1. Op die manier past ze in de verhouding 2 : 1. In het Pythagorese denken is er geen plaats voor 'een getal' , laat staan dat het een esthetisch ideaal zou zijn.
- Slechts in de kringen van Plato, door leerlingen als Euxodus (ca. 410 - 350v.Chr.) en dus na de bouw van het Parthenon, werd de leer van de proportionaliteit uitgebreid tot relaties tussen groottes die niet rationaal meetbaar zijn.
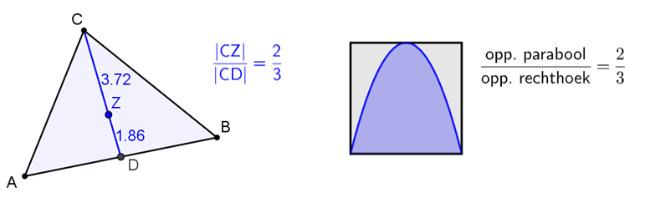
- Die verruiming betekent nog niet dat de focus op verhoudingen van gehele getallen blijft. Zelfs Archimedes publiceert 3 eeuwen later nog nadrukkelijk over de talrijke verhoudingen 1 : 2 : 3 in de meetkunde.
| Pythagoras | ca. 570 v.Chr. - 500 v.Chr. |
| Parthenon | 447 v.Chr. - 437 v.Chr. |
| Plato | ca. 427 v.Chr. - 347 v.Chr. |
| Eudoxus | ca. 400 v.Chr. - 340 v.Chr. |
| Euclides | actief rond 300 v.Chr. |
| Archimedes | ca. 287 v.Chr. - 212 v.Chr. |
modulair systeem
Waar wij symmetrie louter begrijpen als een vormschema als ABA, betekent het in de Oudheid een innerlijke samenhang van verhoudingen, een modulair systeem waardoor alle delen zijn in te passen in het geheel. De terugvinden van de dactylus in de afmetingen van het Parthenon is hierin dus geen wiskundig geknutsel, maar de logica zelve.
Het gaat hierbij om het zijn van de dingen, niet om een esthetisch schoonheidscriterium dat er moet voor zorgen dat mensen de tempel mooi vinden.
Of (in zijn oude betekenis) symmetrie ook samenvalt met schoonheid, daarover lopen de meningen van diverse filosofische strekkingen erg uiteen. Het bevestigt nogmaals dat we bij het kijken naar een Griekse tempel niet in de eerste plaats naar een schoonheidscriterium moeten zoeken als basis voor een ontwerp.
Wie bedacht de gulden snedeclaim in het Parthenon?
De claim dat het Parthenon is gebouwd naar de gulden snede komt uit een boek van Adolf Zeising in 1854: "Neue lehre von den proportionen des menschlichen körpers, aus einem bisher unerkannt gebliebenen, die ganze natur und kunst durchdringenden morphologischen grundgesetze entwickelt und mit einer volständigen historischen uebersicht der bisherigen systeme begleitet".
Zeising wijst in zijn boek inderdaad als eerste naar de gulden snede in de gevel van het Parthenon, volgens hem het mooiste en volmaaktste werk van de Griekse architectuur. Hij vermeldt ook de hoogte en lengte in voet:
- breedte = 107 voet
- hoogte = 65 voet
- som = 172 voet

