Kapitel
₉Extreme Verteilung der 8 Punkten auf der Kugel
Extreme Verteilung der 8 Punkten auf der Kugel/Eight-point models on the surface of a sphere and their Extreme distributions.
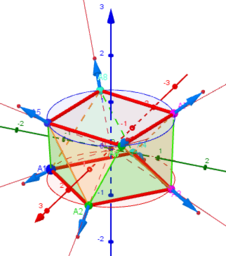
Betrachten Sie als Modell ein System von 8 Punkten auf der Oberfläche einer Kugel mit zwei Freiheitsgraden. 8 Punkte bilden zwei parallele Quadrate. Die
kann relativ zueinander drehen:
der Winkel →α x-Parameter,
der Abstand zwischen ihnen kann sich ändern:
der Neigungswinkel →θ y-Parameter.
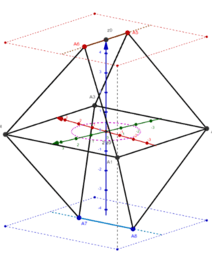
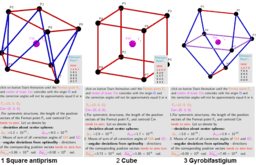
Für bestimmte Parameterwerte können bekannte Körper erhalten werden: Würfel und quadratisches Antiprisma. Seine 8 Seitenflächen sind alles gleichseitige Dreiecke, die alle gleich groß sind.
Als Maß für "Chaos" wählen wir die folgenden Eigenschaften von geometrischen Körpern:
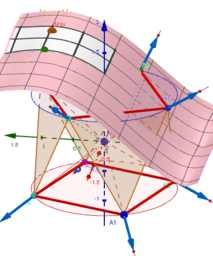
Gesamtabstand. Die Summe der gegenseitigen Abstände aller Punktpaare auf der Kugeloberfläche.
Gesamtfläche. Die Fläche der gesamten Oberfläche des gebildeten Polyeders.
Gesamtvolumen. Körpervolumen.
Die Aufgabe besteht darin,
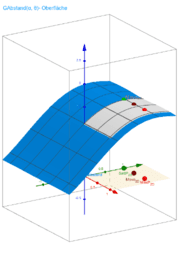
-ermitteln die Abhängigkeiten dieser Eigenschaften von den Parametern α und θ,
-herauszufinden, welche Körpern entsprechen kritischen Punkten dieser drei Oberflächen.
Fazit:
- In den Fällen Gesamtabstand(α, θ) und Gesamtfläche(α, θ) haben die beide Funktionsflächen (im Bereich ihrer Definition) einen Sattelpunkt, der demselben Körper entspricht - dem Würfel.
-Alle drei Funktionsflächen haben kritische Punkte -lokaler Maxima. Die ihnen entsprechenden Strukturen sind sehr ähnlich einem quadratischen Antiprisma.
*From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde
From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp