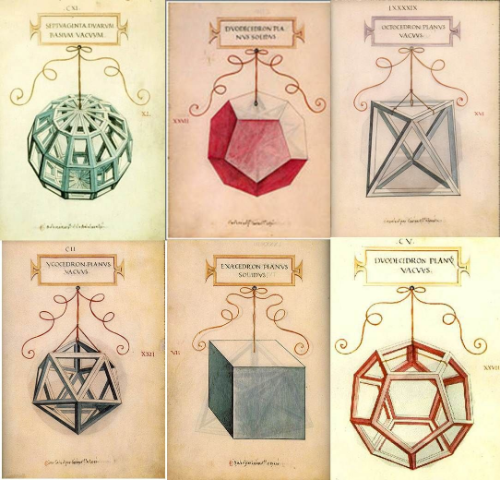
Concepción evolutiva de los cuerpos Geométricos
|
ETAPA |
APORTES DESTACADOS |
CONCEPCIÓN DE AUTORES |
Neolítico 6.000 A.C hasta el año 3.000 A.C | Propiedades de los Poliedros, Bolas neolíticas de piedra labrada | Las propiedades de estos poliedros son conocidas desde la antigüedad clásica, hay referencias a unas bolas neolíticas de piedra labrada encontradas en Escocia 1000 años antes de que Platón hiciera una descripción detallada de los mismos en los elementos de Euclides. El significado de los poliedros se remonta a los primeros estadios de la civilización, Critchlow (1979) da una prueba fehaciente de que ya eran conocidos por los pueblos neolíticos y por las primeras culturas históricas europeas. Diversos historiadores de las Matemáticas (Eves, 1983; Kline, 1992) admiten que las antiguas civilizaciones egipcias y babilónicas tenían conocimiento del cubo, tetraedro y octaedro y que este saber se trasmitiría a Grecia a través de los viajes de Tales y Pitágoras. |
Los pitagóricos | El descubrimiento de los cinco sólidos platónicos. | A la Escuela fundada por él se le atribuye el "descubrimiento" de los cinco sólidos platónicos, creyeron que sólo existen cinco poliedros regulares (aunque la demostración no llegara hasta Euclides), a los cuales llamaron sólidos cósmicos. |
|
Platón | Tetraedros, octaedros, icosaedros, cubos, dodecaedro pentagonal | Se les llegó a atribuir incluso propiedades mágicas o mitológicas; Timeo de Locri, en el diálogo de Platón dice «El fuego está formado por tetraedros; el aire, de octaedros; el agua, de icosaedros; la tierra de cubos; y como aún es posible una quinta forma, Dios ha utilizado ésta, el dodecaedro pentagonal, para que sirva de límite al mundo. |
|
Los elementos de Euclides | Euclides demostró que los poliedros eran sólo cinco | Euclides…fue él quien dio la primera demostración sobre porque dichos poliedros eran sólo cinco y no más, a su vez asoció dichos poliedros con los elementos fundamentales de la Tierra, de manera que al tetraedro le asoció el fuego, al hexaedro la tierra, al octaedro el aire, al icosaedro el agua y por último al dodecaedro el cosmos.
|
El Renacimiento | Artistas matemáticos, surge la geometría proyectiva. | Los llamados artistas matemáticos del Renacimiento manifestaron gran interés por los poliedros. El estudio más completo fue realizado hacia 1480 por Piero della Francesca en su obra "Libellus De Quinque Corporibus Regularibus". |
La cosmología poliédrica de Kepler | Cosmología basada en los cinco sólidos regulares | Kepler fue totalmente seducido por la teoría de Platón y Pitágoras de modo que elaboró una cosmología basada en los cinco sólidos regulares, en la creencia de que estos serían la clave utilizada por el creador para la construcción de la estructura del Universo.
|
En los tiempos modernos | Fórmula de Euler | La famosa Fórmula de Euler que relaciona caras, vértices y aristas de un sólido platónico: «en todo poliedro convexo, el número de vértices menos el número de aristas más el número de caras es igual a dos» (V – A + C = 2), es posible que fuera conocida por Teeteto y por Arquímedes, pero es Descartes quien primero la establece hacia 1635. Euler la obtuvo de nuevo de forma independiente en 1752, dando una sencilla prueba inductiva. |
|
En el arte del siglo XXI | La geometría proporciona importantes argumentos para pinturas y grabados | Gaudí, Escher y Dalí.
Gaudí desarrolló una gran capacidad de utilizar todas las formas geométricas… El autor Escher realiza grandes pinturas y grabaos en los que aparece si peculiaridad artística centrándose en los aspectos matemáticos… Dalí, como para otros muchos artistas, la geometría proporciona importantes argumentos para la realización previa de la obra y su posterior análisis, en particular la Divina Proporción y los poliedros regulares. |

El tratado De la divina proporción (terminado de componer en 1496 y publicado en Venecia en 1509),