Demostración del seno de la suma
En este artículo vamos a demostrar muy detalladamente la fórmula del seno de la suma de ángulos:
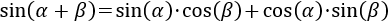
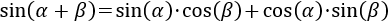
Nota previa
Consideremos la siguiente representación:
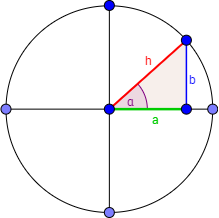 El radio de la circunferencia coincide con la hipotenusa del triángulo: R=h.
El seno, coseno y tangente del ángulo α se definen como
El radio de la circunferencia coincide con la hipotenusa del triángulo: R=h.
El seno, coseno y tangente del ángulo α se definen como
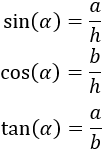 Por tanto, los lados a y b miden
Por tanto, los lados a y b miden
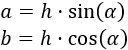 Es decir, los lados son el coseno o el seno multiplicados por la hipotenusa del triángulo con ángulo α.
En la demostración utilizaremos estas igualdades con triángulos cuyas hipotenusas no medirán lo mismo.
Es decir, los lados son el coseno o el seno multiplicados por la hipotenusa del triángulo con ángulo α.
En la demostración utilizaremos estas igualdades con triángulos cuyas hipotenusas no medirán lo mismo.
 El radio de la circunferencia coincide con la hipotenusa del triángulo: R=h.
El seno, coseno y tangente del ángulo α se definen como
El radio de la circunferencia coincide con la hipotenusa del triángulo: R=h.
El seno, coseno y tangente del ángulo α se definen como
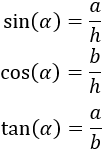 Por tanto, los lados a y b miden
Por tanto, los lados a y b miden
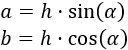 Es decir, los lados son el coseno o el seno multiplicados por la hipotenusa del triángulo con ángulo α.
En la demostración utilizaremos estas igualdades con triángulos cuyas hipotenusas no medirán lo mismo.
Es decir, los lados son el coseno o el seno multiplicados por la hipotenusa del triángulo con ángulo α.
En la demostración utilizaremos estas igualdades con triángulos cuyas hipotenusas no medirán lo mismo.Demostración
Nos apoyaremos en la siguiente representación (donde R será 1 sin pérdida de generalidad):
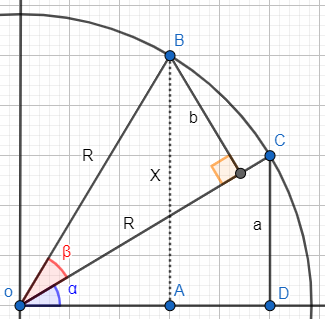 Como el radio de la circunferencia es R=1, entonces
Como el radio de la circunferencia es R=1, entonces
 Como el radio de la circunferencia es R=1, entonces
Como el radio de la circunferencia es R=1, entonces
- El segmento a es el seno ángulo α.
- El segmento b es el seno del ángulo β.
- El segmento X (segmento discontinuo) es el seno del ángulo α+β.
Trazamos el segmento mm paralelo al segmento a:
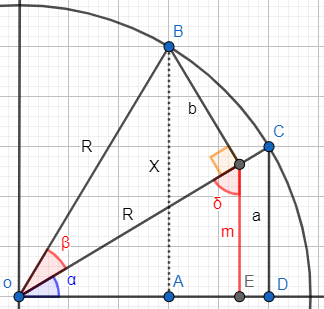 El ángulo δ que aparece mide δ=90∘−α. Esto se debe a que los dos otros ángulos del triángulo miden α y 90∘ y la suma de los tres ángulos debe ser 180∘:
δ=180∘−α−90∘
δ=90∘−α
Teniendo en cuenta la introducción, el lado mm del triángulo es
El ángulo δ que aparece mide δ=90∘−α. Esto se debe a que los dos otros ángulos del triángulo miden α y 90∘ y la suma de los tres ángulos debe ser 180∘:
δ=180∘−α−90∘
δ=90∘−α
Teniendo en cuenta la introducción, el lado mm del triángulo es
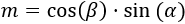 Nota: cos(β) multiplica al seno porque es la hipotenusa del triángulo.
Nota: cos(β) multiplica al seno porque es la hipotenusa del triángulo.
 El ángulo δ que aparece mide δ=90∘−α. Esto se debe a que los dos otros ángulos del triángulo miden α y 90∘ y la suma de los tres ángulos debe ser 180∘:
δ=180∘−α−90∘
δ=90∘−α
Teniendo en cuenta la introducción, el lado mm del triángulo es
El ángulo δ que aparece mide δ=90∘−α. Esto se debe a que los dos otros ángulos del triángulo miden α y 90∘ y la suma de los tres ángulos debe ser 180∘:
δ=180∘−α−90∘
δ=90∘−α
Teniendo en cuenta la introducción, el lado mm del triángulo es
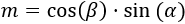 Nota: cos(β) multiplica al seno porque es la hipotenusa del triángulo.
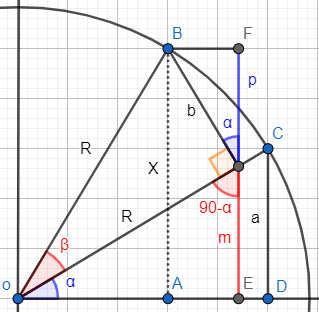
Nota: cos(β) multiplica al seno porque es la hipotenusa del triángulo.Prolongamos el segmento mm obteniendo el segmento p (el segmento mm no cambia):
 Observando la figura,
Observando la figura,
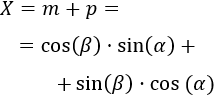 Como queríamos demostrar.
Como queríamos demostrar.
 Observando la figura,
Observando la figura,
- El segmento X mide lo mismo que la suma de los lados m y p.
- El nuevo ángulo representado mide α porque junto con los ángulos 90∘ y 90∘−α debe sumar 180∘.
- Teniendo en cuenta la introducción, el lado p del triangulo superior es
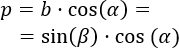
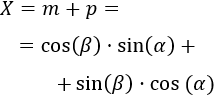 Como queríamos demostrar.
Como queríamos demostrar.