Solve Oblique Quick Quiz
Description
Here you need to choose the formula to find the red dashed value given the solid green highlighted values. The derivation of the equations is shown below. Your goal should be to get twenty correct answers in 2 minutes. The timer starts as soon as you choose your first formula. This is the first step in solving a triangle. You could then use other formulas for finding additional values using your new known values to get all six values of a triangle. In this activity an unknown angle is 'C' and an unknown side length is 'c'. The other sides are 'a' or 'b' and other corresponding angles are 'A' or 'B'.
Solving Oblique Triangles
Solving Oblique Triangles
Solving a triangle means to find lengths of sides and interior angles of a triangle given some of the triangle side lengths or angles. For a right triangle you can use the definitions of the trigonometric functions, but without a right angle you need to use the Law of Sines, Law of Cosines or Interior Angle Sum.
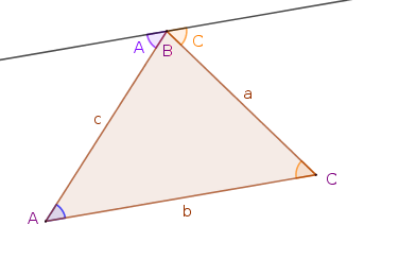
Generally, you need to know three parts of the triangle to find the others. In this applet the known parts are highlighted in green while the part to find is highlighted with red dashed lines. A part can be the measure of an interior angle the the length of a side.
Part Labels
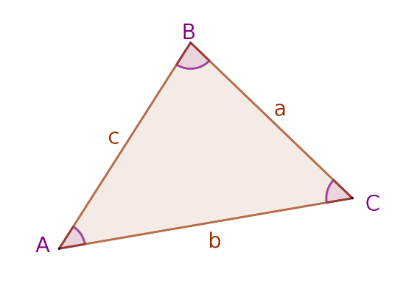
To identify parts of an oblique triangle lower and upper case letters a, b and c are used. A lower case letter represents the length of a side while an upper case letter represents and interior angle. Also, the angle 'A' is opposite the side 'a' as are the other angle side pairs. This is shown as the triangle ABC below.
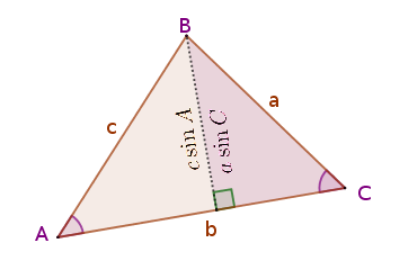
Law of Sines
The Law of Sines can be proven by dropping a perpendicular from one of the corners to the opposite side as shown below. The length of the perpendicular line can be determined from the resulting right triangles on either side of the line. The equal lengths then result in or rewritten as or . Drawing the perpendicular line to the other sides results in similar equations.
To use the Law of Sines you need to know an angle measure and the opposite side length. Then knowing another angle measure you can find its opposite side length or knowing another side length you can find its opposite angle measure.
For the purpose of this applet the known angle side pair is always 'a' and 'A' while the other known value is 'c' or 'C' and the unknown opposite value is also 'C' or 'c'.
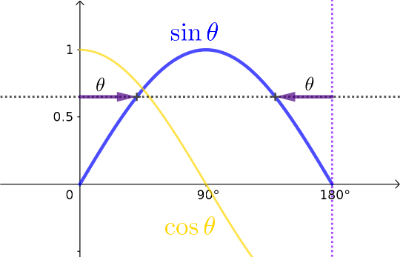
There is a caution with the Law of Sines for finding an angle. The interior angle of a triangle will always be between 0 and 180 degrees, but because Sine has two equal values in this range. This can be seen in the figure below. The angle returned by most Sine functions is equal or less than 90 degrees so you need to consider the obtuse angle as another possible solution. For these triangles it should be obvious which solution to keep.
Law of Cosines
The Law of Cosines can be found in a similar manner by adding a perpendicular line. The point on the line is shown as 'D' below. The length of segment is then and using the Pythagorean Theorem on the triangle on the left results in
which after multiplying out the terms results in . Then noting the identity , this simplifies to which is the Law of Cosines. Note that if then and you have the Pythagorean Theorem.
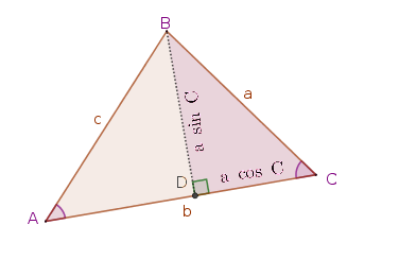
You use the Law of Cosines when you know two sides and the angle between them to find the length of the side opposite the angle. Or use it when you know the lengths of all three sides to find the angle opposite any one of the sides. For this activity the unknown side will be 'c' or the unknown angle will be 'C'.
Angle Sum
The interior angles of a triangle add to a straight angle or . This can be shown by drawing a line parallel to one side through the opposite vertex. Since opposite interior angles between parallel lines are congruent it can be seen that the angles A+B+C add to a straight line or 180o.