icosahedron as planar graph
Leonardo da Vinci (1452-1519)
Leonardo da Vinci made illustrations of solids for Luca Pacioli's 1509 book The Divine Proportion.
These are the first illustrations of polhedra ever in the form of "solid edges", allowing one to see through to the structure. However, it is not clear whether Leonardo invented this new form or whether he was simply drawing from "life" a series of wooden models with solid edges which Pacioli designed.
One of these depicted solids is the icosahedron with 20 equilateral triangles as faces.
drag the grey points
Drag the grey points of the tetrahedron on the left to the graph on the right, so that to top of the icosahedron matches the blue point of the graph and the edges don't cross.
The icosahedron is one of 5 Platonic graphs. These solids have congruent vertices, faces, edges and angles.
In the planar draing and the graph you can clearly see that a tetrahedron has got 4 vertices, 6 sides and 4 faces.
This follows Euler's formula. Euler stated that convex polyhedra, with v the number of vertices, e the number of edges and f the number of faces, always follow the rule v - e + f = 2.
For a icosahedron we get 12 - 30 + 20 = 2.
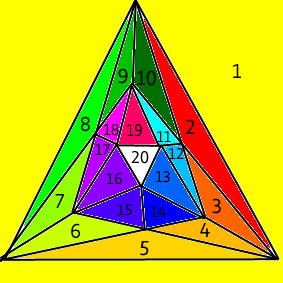
twenty faces
In the following picture the different faces are numbered and colored, so that you can clearly see and distinguish the 20 faces of a icosahedron.
Remark that the outer triangle is regarded as triangle number 1.