UNA CONDIZIONE SUFFICIENTE PER L'EQUIVALENZA
1) Nel disegno sono raffigurati un triangolo ABC di area
e un quadrato DEFG di area
ISTRUZIONI | STRUMENTO | |
| Sull'asse z (che è colorato in blu) disegna il punto P di coordinata 4 | Punto |  |
| Disegna la retta r passante per P e parallela all'asse x (che è colorato in rosso) | Retta parallela |  |
| Prendi un punto V e un punto U sulla retta r. | Punto |  |
| Disegna la piramide avente come base il triangolo ABC e come vertice V e la piramide avente come base il quadrato DEFG e come vertice U. | Piramide | 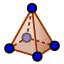 |
3) Le due piramidi hanno la stessa area di base e la stessa altezza, che è data dalla distanza tra il piano xy e il punto
ISTRUZIONI | STRUMENTO | |
| Sull'asse z disegna il punto Q di coordinata 1,5 | Punto |  |
| Disegna il piano k passante per Q e parallelo al piano xy. Nascondi gli assi cartesiani e il punto Q | Piano parallelo |  |
| Interseca il piano k con ciascuna delle facce laterali delle due piramidi e indica i punti di intersezione con A', B', C', D', E', F' | Interseca due superfici | 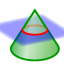 |
| Disegna il triangolo A'B'C' e il quadrilatero D'E'F'G' | Poligono |  |
5) Per le proprietà delle piramidi il triangolo ABC e il triangolo A'B'C' sono
Analogamente: il quadrato DEFG e il quadrilatero D'E'F'G' sono
ISTRUZIONI | STRUMENTO | |
| Disegna la retta s perpendicolare al piano xy passante per V e la retta t perpendicolare al piano xy passante per U | Retta perpendicolare |  |
| Trova le intersezioni H, H' della retta s rispettivamente con il piano xy e con il piano k e le intersezioni K, K' della retta t con il piano xy e con il piano k. Nascondi le rette s, t | Intersezione |  |
| Disegna il segmento VH (che passa per H') e il segmento UK (che passa per K') | Segmento |  |
7) I segmenti VH, UK sono congruenti perchè sono le
8) I segmenti HH', KK' sono congruenti perchè uguali alla
tra il piano xy e il piano k che sono tra loro
9) I segmenti VH' e UK' risultano congruenti per
10) Per le proprietà delle piramidi il rapporto tra l'area del triangolo ABC e l'area del triangolo A'B'C' è uguale a
11) Analogamente il rapporto tra l'area di DEFG e l'area D'E'F'G' è uguale a
12) Dalle uguaglianze 9), 10) 11) si ricava l'uguaglianza per la proprietà
13) Dall'uguaglianza tra le aree dei poligoni ABC, DEFG e dalla 12) si deduce che A'B'C' e D'E'F'G' hanno la stessa area. Le sezioni delle due piramidi con un piano parallelo alla base sono quindi