Matriz simétrica y antisimétrica
Definición de matriz simétrica y antisimétrica y sus propiedades.
Definición de matriz simétrica
Sea A una matriz cuadrada de dimensión mxm. Entonces, A es simétrica si igual a su matriz traspuesta:
Ejemplo
Ejemplo de matriz simétrica de dimensión 3:
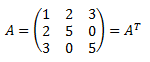
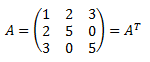
Propiedades de las matrices simétricas
- La inversa de una matriz simétrica regular es simétrica.
- La matriz adjunta de una matriz simétrica es también simétrica.
- La suma de matrices simétricas es una matriz simétrica. El producto lo es si, y sólo si, también es conmutativo.
- Los autovalores (valores propios) de una matriz cuadrada, real y simétrica son reales.
- Autovectores (vectores propios) de autovalores distintos de una matriz cuadrada y real son ortogonales.
- Una matriz cuadrada y real, A, es simétrica si, y sólo si, es diagonalizable mediante una matriz de paso ortogonal, Q. Es decir, .
- Toda matriz cuadrada A cumple que A + AT es simétrica.
Matriz antisimétrica
Una matriz cuadrada es antisimétrica si su traspuesta es igual a su opuesta:
Propiedades
- Toda matriz cuadrada A cumple que A - AT es antisimétrica.
- Toda matriz cuadrada puede expresarse como suma de una matriz simétrica y de una antisimétrica.
Enlaces de Álgebra Matricial
- Conceptos básicos de Matrices
- Matrices Equivalentes: operaciones elementales y formas escalonadas
- Concepto de la matriz inversa: definición, propiedades y métodos
- Matrices Especiales: identidad, diagonal, triangular, traspuesta, adjunta, simétrica, definida positiva, diagonalmente dominante, Hessenberg
- Sistemas de Ecuaciones y Matrices (teoría)
- Determinante, Rango y Menores de una Matriz y Teorema de Rouché-Frobenius
- Diagonalización de Matrices
- Suma de matrices y Matriz Transpuesta
- Producto de Matrices
- Potencias de Matrices
- Matriz Inversa por Adjunción
- Determinantes de matrices con parámetros
- Ejercicios teóricos de matrices (demostraciones)