10-05-23 Properties of Rigid Transformations
I. Intro to the toolbar and transformations with GeoGebra.
a. Translate triangle ABC along the vector that takes A to D.
*Select the vector tool 
and draw a vector starting at point A and ending at point D. Then, select the translate by vector tool 
, click on triangle ABC, and then click on the vector.
b. Reflect triangle ABC over line m.
*Select the reflect about line tool 
, click on triangle ABC, then select line m.
c. Rotate triangle ABC 70 degrees clockwise around point G.
*Select the rotate around point tool 
, click on triangle ABC, then click on point P. Type in 70 degrees and make sure clockwise is selected.
*If you use the move tool 
, note how you can change things dynamically. As an example, select one of the points on your line of reflection, and observe what happens.
and draw a vector starting at point A and ending at point D. Then, select the translate by vector tool , click on triangle ABC, and then click on the vector.
b. Reflect triangle ABC over line m.
*Select the reflect about line tool , click on triangle ABC, then select line m.
c. Rotate triangle ABC 70 degrees clockwise around point G.
*Select the rotate around point tool , click on triangle ABC, then click on point P. Type in 70 degrees and make sure clockwise is selected.
*If you use the move tool , note how you can change things dynamically. As an example, select one of the points on your line of reflection, and observe what happens. II. Measuring line segments
a. Measure the distance of segment AB. Select the distance measuring tool 
, then select point A followed by point B. Note that if you grab the move tool , you can drag the label to a new location.
b. Repeat the process above to measure segment CE and segment ED.
, then select point A followed by point B. Note that if you grab the move tool , you can drag the label to a new location.
b. Repeat the process above to measure segment CE and segment ED. III. Measuring angles
a. Measure angle ABC.
*Select the angle measure tool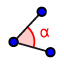 
, then select points A, B, and C in that order. Note that you must select points clockwise in GeoGebra to get the angles measured correctly.
b. Measure all four angles formed by the pair of intersecting lines.
, then select points A, B, and C in that order. Note that you must select points clockwise in GeoGebra to get the angles measured correctly.
b. Measure all four angles formed by the pair of intersecting lines.1. Properties of a Translation
a. Translate triangle ABC along the vector that takes B to G.
**Select the vector tool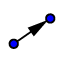 
and draw a vector starting at point B and ending at point G. Then, select the translate by vector tool 
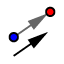, click on triangle ABC, and then click on the vector.
b. Draw another vector from point A to A', and from C to C'. You should now have three sets of vectors, each connecting a pair of corresponding points. Measure the distance of each vector by using the distance measuring tool , and selecting each pair of corresponding points (as an example, click on A followed by A' with the tool selected).
and draw a vector starting at point B and ending at point G. Then, select the translate by vector tool , click on triangle ABC, and then click on the vector.
b. Draw another vector from point A to A', and from C to C'. You should now have three sets of vectors, each connecting a pair of corresponding points. Measure the distance of each vector by using the distance measuring tool , and selecting each pair of corresponding points (as an example, click on A followed by A' with the tool selected). 2. Properties of a Reflection
a. Reflect quadrilateral ABCD over line v.
*Select the reflect about line tool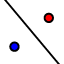 
, click on quadrilateral ABCD, then select line v.
b. Pick two pairs of corresponding points, say B and B', and C and C' and draw a line segment 
between them. Select the point tool 
, and mark each intersection point formed between the line of reflection and your lines connecting your corresponding points.
c. Measure the distance from the line of reflection to each pair of corresponding points using the distance tool . As an example, you are measuring the distance from the line of reflection to B and the distance from the line of reflection to B'.
d. Pick one of your lines connecting a pair of corresponding points, and measure the angle formed between that line and your line of reflection using the angle measure tool .
, click on quadrilateral ABCD, then select line v.
b. Pick two pairs of corresponding points, say B and B', and C and C' and draw a line segment between them. Select the point tool , and mark each intersection point formed between the line of reflection and your lines connecting your corresponding points.
c. Measure the distance from the line of reflection to each pair of corresponding points using the distance tool . As an example, you are measuring the distance from the line of reflection to B and the distance from the line of reflection to B'.
d. Pick one of your lines connecting a pair of corresponding points, and measure the angle formed between that line and your line of reflection using the angle measure tool .
3. Properties of a Rotation
a. Rotate triangle ABC around point P with an angle measure and direction of your choosing. Keep your angle measures less or equal to 90 degrees.
**Select the rotate around point tool 
, click on triangle ABC, then click on point P. Type in an angle measure of your choosing, and select either clockwise or counterclockwise.
b. Draw a line segment from C to point P. Then, draw a line segment from C' to P. *You can use any pair of corresponding points, it does not have to be C and C'.
c.Measure the angle formed using the angle measuring tool . *Select your points in a clockwise order.
d. Measure the distance from P to your two corresponding points using the distance tool .
, click on triangle ABC, then click on point P. Type in an angle measure of your choosing, and select either clockwise or counterclockwise.
b. Draw a line segment from C to point P. Then, draw a line segment from C' to P. *You can use any pair of corresponding points, it does not have to be C and C'.
c.Measure the angle formed using the angle measuring tool . *Select your points in a clockwise order.
d. Measure the distance from P to your two corresponding points using the distance tool .
4. Reflections and Rotations: Two Perpendicular Lines
a. Reflect triangle DEF over the y-axis. Then, reflect triangle D'E'F' over the x-axis.
b. Reset your image, then select triangle DEF and rotate 180 degrees around point P.
5. Two reflections and a rotation.
a. Reflect triangle ABC over line m, then reflect triangle A'B'C' over line n.
b. Measure the angle formed by drawing a line segment connecting A to P, and A'' to P. Write this measurement down. c. Now, rotate triangle ABC counterclockwise around P at an angle equal to the angle you just measured in step b.