9-30-24 Intro. to GeoGebra, Rigid Transformations
1. Plotting Points, Line Types, Polygons
Experiment with the following tools below.
Move: 
Point: 
, Intersect: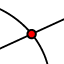 
, Midpoint or Center: 
Line: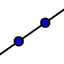 
, Segment: 
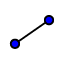, Ray: 
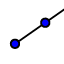, Vector: 
Polygon: 
Angle: 
, Distance or Length: 
Reflect about Line: 
, Rotate around Point: 
, Translate by Vector: 
Point: , Intersect: , Midpoint or Center:
Line: , Segment: , Ray: , Vector:
Polygon:
Angle: , Distance or Length:
Reflect about Line: , Rotate around Point: , Translate by Vector:
2. Measuring Segments and Creating Midpoints.
a. Measure the length of segment AB. Select the Distance or Length tool . Then, select point followed by point B. Alternatively, you can simply select the Distance or Length tool and click on the line segment. Select the move tool and drag points A and or B. Note how the measurement between those two points changes in real time.
b. Plot a midpoint on line segment CD. Select the Midpoint or Center tool , and select points C and D. Using the Distance or Length tool 
, measure the distance between C and the midpoint (should be point E) , and then measure the distance between D and the midpoint.
. Then, select point followed by point B. Alternatively, you can simply select the Distance or Length tool and click on the line segment. Select the move tool and drag points A and or B. Note how the measurement between those two points changes in real time.
b. Plot a midpoint on line segment CD. Select the Midpoint or Center tool , and select points C and D. Using the Distance or Length tool , measure the distance between C and the midpoint (should be point E) , and then measure the distance between D and the midpoint. 3. Meausuring angles
a. Measure angle ABC. Select the Angle tool . Select point A followed by point B followed by point C. Alternatively, select point C followed by point B followed by point A. Note how the angle is adjacent to vertex B, and B is always selected second because it is in-between points A and C. Use the move tool to select the angle measure and move so it is easier to see.
b. Measure all angles formed by line segments QT and SU. Using your knowledge of your work from above, measure all angles in the diagram below using the Angle tool 
. Note how you will always select R second. As an example, measure angle QRS by selecting point Q followed by point R followed by point S (or S followed by R followed by Q).
. Select point A followed by point B followed by point C. Alternatively, select point C followed by point B followed by point A. Note how the angle is adjacent to vertex B, and B is always selected second because it is in-between points A and C. Use the move tool to select the angle measure and move so it is easier to see.
b. Measure all angles formed by line segments QT and SU. Using your knowledge of your work from above, measure all angles in the diagram below using the Angle tool . Note how you will always select R second. As an example, measure angle QRS by selecting point Q followed by point R followed by point S (or S followed by R followed by Q). 4. Side-lengths and Angles of a Triangle
a. Draw a triangle below using the Polygon tool . Then, use the angle tool to measure all angles and the Distance or Length tool to measure all sides on your triangle.
b. If you add up all three angle measures in your triangle, what is the sum equal to? Does this change if you change the way your triangle looks?
. Then, use the angle tool to measure all angles and the Distance or Length tool to measure all sides on your triangle.
b. If you add up all three angle measures in your triangle, what is the sum equal to? Does this change if you change the way your triangle looks? 5. Translation by a vector.
a. Translate quadrilateral ABCD. Select the Vector tool , and draw a vector somewhere in the diagram. Select the Translate by Vector tool , select ABCD by clicking inside the quadrilateral, then click somewhere on the vector (along the line not on an endpoint).
b. Use the move tool to drag the vector, and note what happens to your image.
, and draw a vector somewhere in the diagram. Select the Translate by Vector tool , select ABCD by clicking inside the quadrilateral, then click somewhere on the vector (along the line not on an endpoint).
b. Use the move tool to drag the vector, and note what happens to your image. 6. Reflecting over a line.
a. Select the line segment tool and draw a line somewhere in the diagram. Select the Reflect about Line tool , select triangle ABC by clicking inside the triangle, then select your line.
b. Drag your line around the diagram using the Move tool , and note what happens.
and draw a line somewhere in the diagram. Select the Reflect about Line tool , select triangle ABC by clicking inside the triangle, then select your line.
b. Drag your line around the diagram using the Move tool , and note what happens. 7. Rotation
a. Select the Point tool and place a point somewhere in the diagram. Select the Rotate around Point tool , select triangle ABC by clicking inside the triangle, then select your plotted point. A dialogue box will pop up, allowing you to choose the number of degrees triangle ABC will rotate and what direction (clockwise or counterclockwise).
b. Drag your point around using the Move tool . What happens when you move the center of rotation closer to the triangle or further away? What if you place the point inside the shape or on a vertex?
and place a point somewhere in the diagram. Select the Rotate around Point tool , select triangle ABC by clicking inside the triangle, then select your plotted point. A dialogue box will pop up, allowing you to choose the number of degrees triangle ABC will rotate and what direction (clockwise or counterclockwise).
b. Drag your point around using the Move tool . What happens when you move the center of rotation closer to the triangle or further away? What if you place the point inside the shape or on a vertex? 8. Triangle Proof, Angle Sum Theorem
a. Construct a midpoint on side AB. Select the Midpoint or Center Tool , then select point A followed by point B. You should now see a red point on your triangle labeled D.. Select the Rotate around Point tool , select triangle ABC by clicking on the inside of the shape, then select point D. A dialogue box should pop up for a rotation; type in 180 degrees and click okay. You have now rotated triangle ABC about the midpoint of side AB.
b. Repeat the process above for side BC. Construct the midpoint of side BC using the same process above, then rotate triangle ABC 180 degrees around the midpoint.
c. Repeat the process above for side AC.
d. Measure all of the angles in all three triangles. There is a shortcut using the Angle tool in GeoGebra; for any polygon if you click inside of the shape with the angle tool all interior angles are automatically measured. Measure the angles in all three triangles, then use the Move tool to drag the angle measurements so they are easier to read.
, then select point A followed by point B. You should now see a red point on your triangle labeled D.. Select the Rotate around Point tool , select triangle ABC by clicking on the inside of the shape, then select point D. A dialogue box should pop up for a rotation; type in 180 degrees and click okay. You have now rotated triangle ABC about the midpoint of side AB.
b. Repeat the process above for side BC. Construct the midpoint of side BC using the same process above, then rotate triangle ABC 180 degrees around the midpoint.
c. Repeat the process above for side AC.
d. Measure all of the angles in all three triangles. There is a shortcut using the Angle tool in GeoGebra; for any polygon if you click inside of the shape with the angle tool all interior angles are automatically measured. Measure the angles in all three triangles, then use the Move tool to drag the angle measurements so they are easier to read. 9. Quadrilateral Angle Sum Theorem
a. Construct a midpoint on side AD. Select the Midpoint or Center Tool , then select point A followed by point D. You should now see a red point on your triangle labeled E. Select the Rotate around Point tool , select quadrilateral ABCD by clicking on the inside of the shape, then select point E. A dialogue box should pop up for a rotation; type in 180 degrees and click okay. You have now rotated quadrilateral ABCD about the midpoint of side AD.
b. Repeat the process above for side A'B'. Construct the midpoint of side A'B' using the same process above, then rotate quadrilateral ABCD 180 degrees around the midpoint.
c. Repeat the process above for side B''C''.
d. Measure all of the angles in all four quadrilaterals. There is a shortcut using the Angle tool in GeoGebra; for any polygon if you click inside of the shape with the angle tool all interior angles are automatically measured. Measure the angles in all four quadrilaterals, then use the Move tool to drag the angle measurements so they are easier to read.
, then select point A followed by point D. You should now see a red point on your triangle labeled E. Select the Rotate around Point tool , select quadrilateral ABCD by clicking on the inside of the shape, then select point E. A dialogue box should pop up for a rotation; type in 180 degrees and click okay. You have now rotated quadrilateral ABCD about the midpoint of side AD.
b. Repeat the process above for side A'B'. Construct the midpoint of side A'B' using the same process above, then rotate quadrilateral ABCD 180 degrees around the midpoint.
c. Repeat the process above for side B''C''.
d. Measure all of the angles in all four quadrilaterals. There is a shortcut using the Angle tool in GeoGebra; for any polygon if you click inside of the shape with the angle tool all interior angles are automatically measured. Measure the angles in all four quadrilaterals, then use the Move tool to drag the angle measurements so they are easier to read. 10. Creating a rotation with a slider
a. Create a slider that will allow you to adjust the rotation of triangle ABC from 0 to 360 degrees.
i. Select the Slider tool 
, then click somewhere in the diagram. A dialogue box will pop up. Then, where is says =45, change (alpha) to a normal letter, lets say letter v.
ii. Select the Rotate around Point tool , select triangle ABC, then select point P. When the dialogue box pops up, under angle, delete the number of degrees, type in the letter v.
Your triangle will now rotate based on the slider, use the Move tool to adjust the slider.
, then click somewhere in the diagram. A dialogue box will pop up. Then, where is says =45, change (alpha) to a normal letter, lets say letter v.
ii. Select the Rotate around Point tool , select triangle ABC, then select point P. When the dialogue box pops up, under angle, delete the number of degrees, type in the letter v.
Your triangle will now rotate based on the slider, use the Move tool to adjust the slider.