Introducción: escáner de color dinámico
Esta actividad pertenece al libro de GeoGebra Variable compleja.
Introducción a la coloración punto por punto de una superficie
La coloración sigue el método que combina el rastro y el color dinámico, tal como expliqué en el foro de GeoGebra en 2009 y 2011. Para detalles acerca de este método, se puede consultar este libro GeoGebra y este artículo, así como este otro artículo de Juan Carlos Ponce. Como novedad, ahora no se colorea sobre un rectángulo plano, sino sobre la superficie mencionada, por lo que basta el canal H (matiz) para representar el argumento principal (fase) y se puede prescindir del canal L (luminosidad) para representar el módulo.
También se puede usar el código de color RGB, como en la siguiente imagen, que recoge la vista en el plano complejo XY de la representación tridimensional de la función compleja f(z) = z5 + 1, usando este código para la parte imaginaria de f(z), tal como se muestra en la siguiente actividad. La frontera amarillo/rojo indica un cambio del signo de esta parte imaginaria.
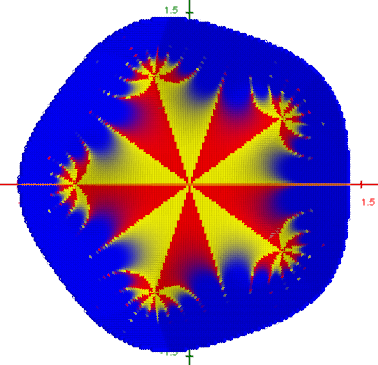
Nota: He sugerido en el foro de GeoGebra el interés que supondría integrar un método similar de coloración dinámica punto por punto en el comando Superficie.
Para favorecer la visualización, es altamente recomendable limitar el ancho de los intervalos de dominio ([x1, x2], [y1, y2]) de las variables del plano complejo XY a unas 4 unidades, aproximadamente. En caso de intervalos mayores, se puede hacer un alejamiento previo con el zoom (pulsando en la vista 3D y girando la rueda del ratón). He optado, en un compromiso entre velocidad y calidad, por crear un escáner de color dinámico con solo 400 puntos. Creo que son sufientes en la mayoría de las ocasiones. Si se desea mayor calidad, se puede descargar la construcción y reducir el tamaño de cada punto al tiempo que se eleva el número de puntos o se reduce el ancho de los intervalos.