Kapitel
Integralrechnung- Ober- und Untersummen
Im Buch (Mathematik verstehen 8, öbv) findest du auf S. 11- 17 Informationen und Beispiele zum Thema "Unter-und Obersummen- Integral".
In einem Intervall [a;b] bezeichnet man die von der Funktion f festgelegte Fläche als A(a,b). Die Funktion f nimmt im Intervall [a;b] nur positive Funktionswerte an.
Näherungsweise kann man die Fläche bzw. den Flächeninhalt A(a,b) mithilfe der Summe von Rechtecken berechnen. Dabei wird das Intervall [a; b] in Teilintervalle zerlegt. Der Flächeninhalt eines dieser Rechtecke wird mithilfe der dem Wert der Intervallbreite (Breite) und des jeweiligen Funktionswerts (Höhe) berechnet.
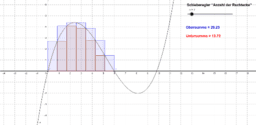
Untersumme U : Summe der eingeschriebenen Rechtecke = Untere Schranke von A(a;b)
Obersumme O : Summe der umgeschriebenen Rechtecke = Obere Schranke von A(a;b)
Je kleiner die Teilintervallbreite desto geringer ist die Differenz O-U. Je größer die Anzahl n der Teilintervalle von [a;b] desto geringer ist die Differenz O-U.
D. h je mehr Rechtecke ein-bzw umgeschrieben werden desto genauer ist U bzw. O ein Näherungswert für A(a;b).
Es gibt daher genau einen Wert I der zwischen U und O liegt, der den Fächeninhalt A(a; b) genau beschreibt. Diese Zahl I nennt man Integral der Funktion f im Intervall [a; b]