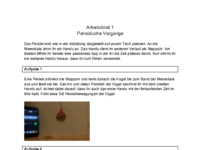
Periodische Vorgänge ( Fadenpendel )
Kurzinformation
- Thema: Einführung von periodischen Vorgängen
- 6. Klasse - Mathematik
- Dauer: 2 - 3 Einheiten
- SchülerInnenmaterial: 2 Arbeitsblätter siehe unten
- Spezielle Materialien: 2 x Handy, Mathematisches Pendel ( Bastelanleitung )
Vorwissen und Voraussetzungen
Die Schüler und Schülerinnen wissen
- wie eine Wertetabelle erstellt wird
- wie mit Hilfe einer Wertetabelle einen Funktionsgrafen erstellt.
- wie man Funktionswerte im Koordinatensystem liest
Lernergebnisse und Kompetenzen
In den 2-3 Unterrichtssequenzen sollen die SuS durch forschendes, entdeckendes lernen die Wichtigkeit von periodischen Vorgängen in Natur und Technik erfassen.
- Daten graphisch darstellen
- periodische Vorgänge in Natur und Technik nennen.
- periodische Vorgänge mit Sinus und Cosinus Funktion modellieren.
- Merkmale wie Amplitude und Periodendauer aus dem Funktionsgrafen ablesen.
Unterrichtsablauf
1. Einheit
Am Beginn der ersten Unterrichtseinheit wird kurz der Ablauf der Unterrichtseinheit erläutert. Die Schüler und Schülerinnen erhalten ein Aufgabenblatt auf dem der Ablauf der Unterrichtseinheit sowie die zu erledigenden Aufgaben Schritt für Schritt erklärt sind. Zusätzlich zum Aufgabenblatt erhält jede Gruppe ( bestehend aus 2-3 SuS ) ein Fadenpendel ( siehe Unterrichtsmaterial ). Das Aufgabenblatt wird mit Zuhilfenahme von Fadenpendel und Smartphone bearbeitet. Falls das Aufgabenblatt nicht fertig bearbeitet werden kann, werden die übrigen Aufgaben als Hausübung aufgegeben.
2. Einheit
Zu Beginn der zweiten Einheit wird das Arbeitsblatt im Plenum besprochen. ( Welche Informationen können aus dem Diagramm abgelesen werden, wo kommen ebenfalls periodische Funktionen in der Natur bzw. Technik vor, haben periodische Funktionen immer die selbe Gestallt?) . Danach wird im fragend entwickelndem Unterrichtsgespräch den SuS gezeigt, dass sie bereits periodische Funktionen kennen und diese zur Modellierung herangezogen werden können. Hier wird nun wieder das Aufgabenblatt aus der 1. Unterrichtsstunde herangezogen. Die SuS Modellieren mit Geogebra eine Sinus Funktion. Anschließende wird ein Aufgabenblatt zu den Parametern der Trigonmetrischen Funktionen mit Hilfe von Geogebra bearbeitet.
Aktivität 1 Erklärung (5-10 min )
Die Lehrkraft erklärt kurz den Ablauf der Unterrichtseinheit und teilt die Arbeitsunterlagen sowie die benötigten Fadenpendel aus.
Aktivität 2 Arbeitsblatt 1 ( 40 min )
Die Schüler und Schülerinnen bearbeiten im 2er bzw. 3er Team das Arbeitsblatt. Falls die Gruppen nicht fertig werden können die Aufgaben 3 & 4 auch zuhause als Hausübung fertig gestellt werden.
Arbeitsblatt1
Sicherung & entwickelndes Unterrichtsgespräch (30min)
In der zweiten Stunde werden die Ergebnisse des Aufgabenblattes besprochen und die wichtigen Begriffe wiederholt. Danach wird im fragend entwickelndem Unterrichtsgespräch den SuS gezeigt, dass sie bereits periodische Funktionen kennen - Sin & Cos und diese zur Modellierung herangezogen werden können.
Aktivität 3 Arbeitsblatt 2 (20min)
Die Schüler und Schülerinnen nehmen nochmals ihre Daten aus dem Experiment zur Hand und übertragen diese in Geogebra. Durch passende Wahl der Parameter wird eine Sinus bzw. Cosinus Funktion an die Messdaten angepasst und die Aufgaben von Arbeitsblatt 2 bearbeitet.
Arbeitsblatt 2
Arbeitsblatt 2 mit Lösungen
Überprüfen des Lernerfolges
Während der Bearbeitung der Arbeitsaufträge kann die Lehrkraft den Fortschritt der einzelnen Schüler und Schülerinnen beobachten. Vereinzelte Aufgaben können von der Lehrkraft abgesammelt und begutachtet und kontrolliert werden. Hier eignet sich vorallem das zweite Arbeitsblatt.
Links zu Materialien und Quellen
Geogebra Applet für Arbeitsblatt 2
https://www.geogebra.org/classic/pdfyf7xb
Quellen:
- Mathematik lehren 2017/204