Juliette Hernando - Démonstration du théorème de Pythagore

Introduction et agencement

Prenons un triangle rectangle et notons a, b et c la longueur de chacun des côtés, a étant l'hypoténuse.

En cliquant sur le bouton SUIVANT, faisons apparaître trois nouveaux triangles parfaitement identiques.

En cliquant à nouveau sur le bouton SUIVANT, faisons également apparaître un carré de côté a.

Ce carré possède une force d'attraction telle qu'en cliquant une dernière fois sur le bouton SUIVANT, nos quatre malheureux triangles sont irrésistiblement attirés par lui et que l'hypoténuse de chacun vient se coller par magie le long de chacun d'un des côtés du carré.

On obtient cette figure et la première étape de la démonstration consiste à prouver que EFGH est un carré.

On va déjà commencer par prouver qu'on a bien un quadrilatère en réussissant à montrer que les points E, I et F sont alignés.

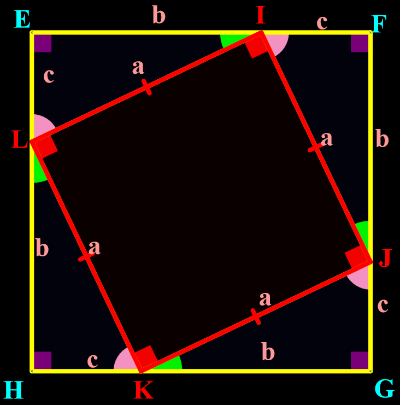
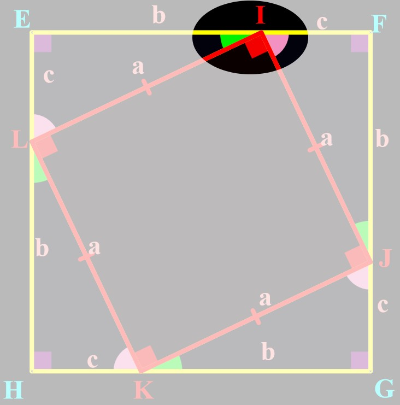
Écrire la mesure de l'angle EIF comme une somme des mesures de trois angles.

Le triangle initial étant un triangle rectangle, que pouvons-nous dire de la somme des mesures de ses deux angles aigus ?

Dans le carré IJKL, quelle est la mesure de l'angle LIJ ?

En déduire la mesure de l'angle EIF.

Que peut-on en déduire pour les points E, I et F ?

De la même façon, on prouve que les points F, J et G sont alignés, que les points G, K et H sont alignés et enfin que les points H, L et E sont alignés, et finalement qu'on est bien en présence d'un quadrilatère EFGH.

Démontrer que ce quadrilatère est un rectangle.

Démontrer enfin que ce rectangle est un carré !

Calculons de deux façons différentes l'aire du carré EFGH.

Quelle formule donne l'aire d'un carré ?

Cochez votre réponse ici

Vérifier ma réponse (3)

Donner une expression de la longueur du côté du carré EFGH.

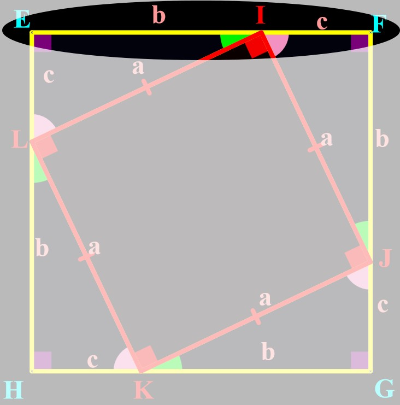
En déduire une expression de l'aire du carré EFGH.

Développer et réduire l'expression obtenue.

Utilisons maintenant une deuxième méthode pour calculer cette aire : l'aire du carré EFGH est la somme de celle du carré IJKL et de celles des quatre triangles rectangles IJF, JKG, KLH et LIE.

Donner l'expression de l'aire du carré IJKL.

Quelle formule donne l'aire d'un triangle rectangle ?

Cochez votre réponse ici

A
B
où et sont les longueurs des deux côtés de l'angle droit
C

Vérifier ma réponse (3)

Donner l'expression de l'aire d'un triangle rectangle.

En déduire une deuxième expression de l'aire du carré EFGH. (Réduire au maximum)

Avec les deux méthodes que l'on vient d'utiliser, on vient de trouver deux formules qui permettent de calculer la même aire du carré EFGH, elles sont donc égales !

Écrire cette égalité et la réduire en simplifiant les termes identiques dans chacun de ses membres.

Juliette Hernando - Démonstration du théorème de Pythagore

Démonstration liée à la vidéo de Juliette Hernando ci-dessous :

Nouvelles ressources

Découvrir des ressources

Découvrir des Thèmes