Locus equations which may need absolute factorization
A regular triangle ABC is given. Where to put point D in order to the sum of two distances between it and the vertices of the triangle will be equal to the distance between it and the third vertex?
GeoGebra can answer this question when using the
LocusEquation[f+g==h,D] command. In fact, it computes the answer at the same time also for the conditions g+h==f and h+f==g.
The answer is the union of two circles. The web version of GeoGebra (as of July 2016) cannot compute the answer because of memory limitations, but the desktop version can: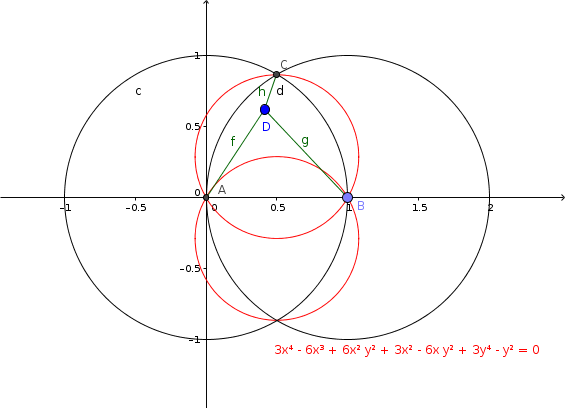
The polynomial of this algebraic curve is a product of two circles, but the y-coordinate of their centers is . That prevents having a factorization with integer coefficients only.
"Factorization" of algebraic curves can be crucial when plotting implicit curves. Plotting the factors separately increases the quality of the plot. In this case, however, factorizaton is not really required: both circles can be seen perfectly.
Absolute factorization (that is a factorization over an algebraic closure of its coefficient field) is not yet implemented in GeoGebra. It's available in some other computer systems like Maple or Singular.
A further example
Holfeld's 24th problem in his Exercitationes Geometricae (1773) also produces a locus equation which can be factorized, but not always over the integers. Try to drag point B to various points, e.g. to (0,4).