예각의 삼각비
[탐구활동 1] 예각의 삼각비를 정의하자.
[질문 1] 점R이 어디있을 때 "높이=sinA"가 되나요?
[질문 2] 점 R이 어디있을 때, "밑변=cosA"가 되나요?
[질문3] 점 R이 [질문1], [질문 2]의 답의 위치에 있을 때, "높이=sinA", "밑변=cosA"가 되는 이유는 무엇때문일까요?
[질문 4] tan A=높이가 되는 점 B의 위치와 그 이유는?
[탐구활동2] 제 예각의 삼각비의 변화를 관찰해 봅시다.
아래 그림에서 슬라이더를 움직여서 각의 크기에 따른 삼각비의 값을 관찰해보세요.
[질문 6] 각이 커져갈수록 cos A의 값은 어떻게 바뀌고 있나요?
[질문 7] 각이 커져갈수록 tan A의 값은 어떻게 바뀌고 있나요?
[마지막 질문] 왜 sin 0°=0, sin 90°=1이라 정할까요?
열심히 공부하며 따라와줘서 고맙습니다.
잘 이해했고 활용할 수 있는지 아래 문제들을 해결하면서 따라와 봅시다.
문제 1-(1) sin 90°×tan30° - cos 90°×tan45°=?
문제 1-(2) sin 45°×cos 0° + cos 45°×sin 0 °=?
<탐구활동> 삼각비표
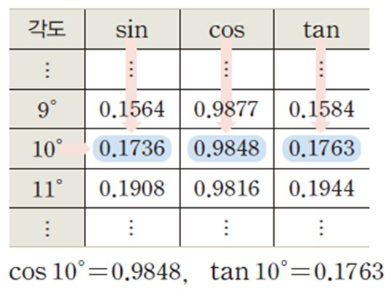
옛 사람들은 삼각비의 값이 필요할 때 아래 그림과 같은 삼각비 표를 이용해서 찾았습니다.
sin 10°라면 아래 표의 왼쪽에서 10°를, 위쪽에서 sin을 찾은 뒤 서로 만나는 값 0.1736을 찾는 방식입니다.
문제 2. 삼각비표를 이용해서 여러 문제를 해결해 봅시다.
문제 2-(1) sin 9°
문제 2-(2) cos 11°
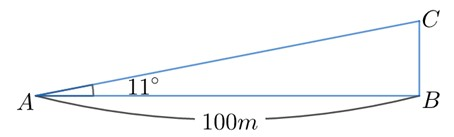
문제 2-(3). 위 직각삼각형에서 삼각비를 이용해 선분 BC의 길이를 구하면?