Würfel, Quader und Prismen
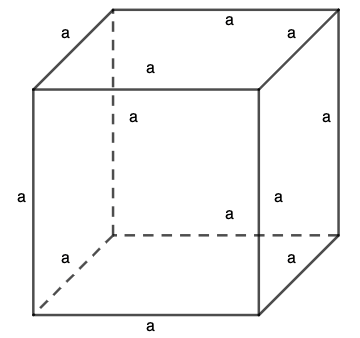
Würfel (Hexaeder)
Die gegenüberliegenden Flächen sind jeweils parallel und deckungsgleich.
Ein Würfel hat:
- 8 rechtwinklige Ecken
- 12 gleich lange Seitenkanten
- 6 quadratische Begrenzungsflächen
Oberfläche:
Hier Spezialfall: alle Flächen gleich
Volumen:
Länge der Raumdiagonale:
Quader
Die gegenüberliegenden Flächen sind jeweils parallel und deckungsgleich.
Ein Würfel hat:
- 8 rechtwinklige Ecken
- 12 Seitenkanten, jeweils vier sind gleich lang und parallel
- 6 rechteckige Begrenzungsflächen
![[size=85]Oberfläche:
[math]O=2G+M[/math]
[math]O=2⋅a⋅b+2⋅a⋅c+2⋅b⋅c[/math]
Volumen:
[math]V=G⋅h[/math]
[math]V=a⋅b⋅c[/math]
Länge der Raumdiagonale:
[math]d=\sqrt{a^2+b^2+c^2}[/math]
[/size]](https://beta.geogebra.org/resource/qmq5hvms/QenhkQRrlImCxzEe/material-qmq5hvms.png)
Netz vom Quader und regelmäßigen Prismen
Prismen
Eigenschaften von Prismen
• Prismen haben zwei zueinander parallele und kongruente (deckungsgleiche) Grundflächen. Die Grundflächen können beliebig viele Ecken haben.
• Die restlichen Begrenzungsflächen sind.
• Sie bilden die Mantelfläche.
Oberfläche:
Volumen:
Da Prismen verschiedene Grundflächen haben können, gibt es hier nur die allgemeine Formel
Eine Übersicht über die verschiedenen Grundflächen bei Prismen findest du bei den Flächen oder Vielecken