van Pythagoras naar ongelijkzwevende stemmingen
Muziekwetenschappers en wiskundigen zoeken oplossingen voor de problemen die zich stellen
met de stemming van Pythagoras en de reine stemming.
We verlopen nog een keer de problemen en verkennen enkele oplossingen die uitgewerkt werden door
Rameau, Werckmeister, Kirnberger en Valotti.
De meesten van hen werkten meer dan een voorstel uit.
Om het hoe en waarom van deze stemmingen beter te begrijpen overlopen we nog even het verhaal vanaf Pythagoras over de reine stemming tot de middentoonstemming.
Pythagoras
| uitgangspunt | Tonen verhouden zich als gehele getallen |
| realisatie | Alle afstanden worden opgebouwd vanuit de reine kwintverhouding 3/2 |
| probleem | Kwinten sluiten niet aan op octaven en tertsen. Een terts die opgebouwd is vanuit een kwint is niet rein en klinkt te hoog. |
| muziek | - veel samenklanken van kwinten. - tertsen worden vermeden |

reine stemming
In de reine stemming wordt de kwintafhankelijkheid van de terts opgegeven.
De afstand do - re is een grote hele toon met verhouding 9/8.
De afstand re - mi is een kleine hele toon met verhouding 10/9.
De verhouding tussen beide noemen we het syntonische komma = 81/80.
| uitgangspunt | De kwintafhankelijkheid van de terts opgegeven. |
| realisatie | Secunde en kwart worden opgebouwd vanuit de reine kwintverhouding 3/2. De terts krijgt de reine verhouding 5/4. Sext en septime worden opgebouwd vanuit de terts. |
| probleem | Een toonladder bestaat uit grote en kleine halve tonen. |
| muziek | Een muziekstuk staat in de toonaard waarin het instrument rein gestemd is. |
middentoonstemming
Door de kwintafhankelijk van tertsen op te geven werden de tertsen wel terug rein, maar sloot men zich op in een toonaard. Een grotere vrijheid tussen toonaarden is slechts mogelijk met tertsen, bepaald door de kwint. De enige mogelijkheid om tertsen terug rein(er) te krijgen is dus de kwint te verkleinen.
Dit noemt men temperen.
De middentoonstemming verlaagt de kwint met 1/4 van een komma.
- Met het komma bedoelen we het syntonisch komma 81/80
- 1/4 van dit komma bereken je als 4√(81/80)
- De kwint verlagen met 1/4e komma bereken je als 3/2 : 4√(81/80)
- De terts is perfect rein.
- De kwint is iets te klein maar wijkt nauwelijks af van de 3/2 verhouding.
- Alle afstanden kunnen berekend worden vanuit de kwint.
- De afstanden C-D en D-E zijn even groot en niet meer groot en klein zoals in de reine stemming.
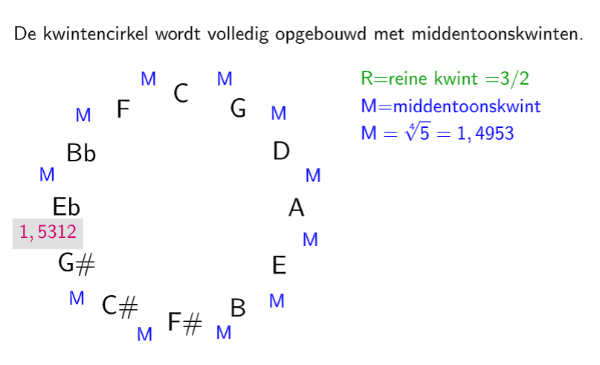
| uitgangspunt | De tertsen moeten afgeleid worden van de kwint en tegelijk rein klinken. |
| realisatie | De kwintverhouding 3/2 wordt verkleind met 1/4e komma tot 4√5 = 1,49535 |
| probleem | De kwintencirkel sluit zeer slecht. De sluitende kwint is veel te groot. Ze wordt wolfskwint genoemd en moet vermeden worden. |
| muziek | Het vermijden van wolfskwint beperkt nog de onafhankelijkheid van toonaarden. |
ongelijkzwevende stemmingen
Alle tertsen rein maken door de kwinten te verkleinen tot de middentoonskwint is niet te verzoenen met een vrijheid van toonaarden. Omdat in de barokmuziek die vraag naar meer harmonische vrijheid groter wordt, moet ook hier weer een compromis gezocht worden.
Dit compromis bestaat er in om het aantal verlaagde kwinten in de kwintencirkel te beperken.
In de 17e en 18e ontwikkelen diverse componisten uiteenlopende stemmingen.
Omdat alle kwinten in de kwintencirkel niet meer gelijk zijn, zullen ook de onderlinge verhoudingen tussen de verschillende toontrappen in verschillende toonaarden niet meer gelijk zijn.
Je kunt dus niet zeggen: "zo klikt deze stemming", maar wel "zo klinkt deze toonaard in deze stemming."
Het uitgangspunt van elke poging is wel steeds hetzelfde:
- zo rein mogelijke tertsen in de meest gebruikte toonaarden
- een zo goed mogelijk aansluitende kwintencirkel om in zo veel mogelijk toonaarden te kunnen spelen.