abstracte concepten en praktijk
portaal van de Vrijdagmoskee in Isfahan
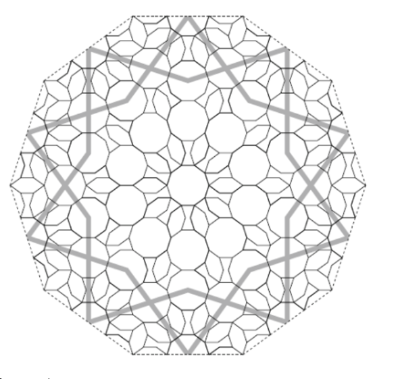
Op een portaal van de Vrijdagmoskee in Isfahan treffen we onderstaand motief aan.
Net zoals op het tympaan en de zwik van de boog op de Darb-e Imam is een motief van kleine tegels ingebed in een eerste laag van grotere girih tegels.
strikt genomen niet zelfgelijkvormig
Je kunt een Penrosebetegeling opbouwen door te vertrekken van één vorm, hierop de opdelingsregels toe te passen en vervolgens de bekomen vormen te vergroten. Dit proces noemen we inflatie.
De Islamitische decorateurs gaan nergens op deze manier te werk. Ze vertrekken van een raamwerk van grote tegels in een configuratie die niet voorkomt in het kleinschaligere motief.
Lu en Steinhardt geven zelf ook toe dat, strikt genomen, het motief dus niet zelfgelijkvormig is 'alhoewel een herhaalde toepassing van de opdelingsregels wel tot een aperiodische vlakvulling leiden'.
Cromwell
En met deze redenering heeft Cromwell het wel wat moeilijk. Het lijkt alsof de decorateur, als hij het zou willen, zou kunnen starten met één tegel en stapsgewijs inflatie toepassen tot het hele te bedekken oppervlak bedekt was. Maar dit is rederenen vanuit moderne, meetkundige abstractie. Bronnen getuigen dat in de Seltsjoekperiode een grondige meetkundige kennis aanwezig was en men zich zeker bewust was van kenmerken van vijf- en tienhoek. Maar begrippen als regelmatige en niet-regelmatige vlakvullingen en inflatie waren niet bekend. Het is dan ook gewaagd om ze zomaar toe te passen op een praktijk van decoraties.
Volgens Cromwell illustreren de Isfahanpatronen, net zoals de voorbeelden uit de Topkapirol de intelligente kennispraktijk opdeling te gebruiken om een kleinschalig patroon te genereren binnen een groter patroon. Dit groter patroon is ook niet zomaar toevallig gekozen. We kunnen de drie motieven op eenzelfde achtergrond zetten van tienhoeken en strikken, een van de oudste en meest alomtgenwoordige strikmotieven waarmee de ambachtsmannen zeer vertrouwd waren.
Linksboven zie je de zwik en rechtsboven het tympaan van de Darb-e Imam. Onderaan zie je de langwerpige pand van het portaal in de Vrijdagmoskee.
herhaalde opdelingsregel in de praktijk niet werkbaar
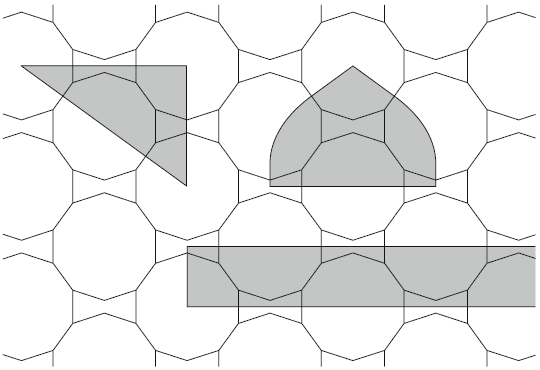
Cromwell berekende de schaalfactor die het gevolg is van de opdelingsregel als (afgerond 8,472).
Alle vormen worden dus meer dan acht keer kleiner per opdeling, wat herhaalde opdeling meteen onwerkbaar wordt. Zo zou het twee keer opdelen van één tienhoek alleen al 15 000 tegels opleveren.
Zijn conclusies zijn:
- Het is mogelijk om met een set girih tegels quasi-periodische betegelingen te creëren via inflatie of pasregels.
- Islamitische artiesten gebruikten opdeling om opmerkelijke, heel verscheidene hiërarchische ontwerpen te produceren (zie Topkapirol en Isfahan)
- Er is geen bewijs van iteratie van opdeling. Er zijn enkel ontwerpen bekend met twee niveaus en dit alleen al om praktische redenen. De schaalfactor is doorgaans erg groot en het te bedekken oppervlak beperkt. Met de opdelingen in de Topkapirol is iteratie zelfs onmogelijk.
- De ontwerpen die bekend zijn, vormen geen bewijs dat de Islamitische kunstenaars zich bewust waren van een proces dat quasi-periodische ontwerpen kan voortbrengen. Sommige zijn periodisch, andere meerlagige ontwerpen zijn hiërarchisch en niet schaalinvariant.
een welbepaald oppervlak decoreren
Cromwell merkt ook op dat artiesten, vaak in de hoeken van een te decoreren oppervlak, durven afwijken van de opdelingsregels. Telkens komt het de esthetiek van het ontwerp ten goede, zodat bv een zeshoek of anders opgedeelde tienhoek beter past in de hoek van een tympaan of zwik van een boog.
De girih tegels en de kunde om een motief op te hangen binnen een groter kader zijn in de handen van een vaardig ontwerper een verbazend middel om op onwaarschijnlijk virtuoze manier een welbepaald beperkt oppervlak te decoreren en steeds weet hij die mogelijkheden te benutten die best passen, terwijl de moderne wiskundige vanuit zijn abstract denkkader begint te analizeren en vaststelt dat de decorateurs 'fouten' maakten in hun ontwerp...
als je in detail kijkt...
Een artikel van Peter Cromwell in Nexus Journal in 2016 is ontnuchterend voor Lu & Steinhard en al wie de overeenkomsten met Penrose maar al te graag voor werkelijkheid neemt.
In een detailanalyse van een zwik van de Vrijdagmoskee in Isfahan komt Cromwell tot de conclusie dat de decorateurs heel pragmatisch omgingen bij het toepassen van het tweelagige ontwerp. Het belangrijkste doel was het opvullen van een vlak. Moest daarbij op verschillende plaatsen een verschillende opdeling gemaakt worden, was dat geen probleem, wanneer een krans van cirkels overlappende tienhoeken zou opleveren, werden achthoekige sterren ipv tienhoekige gecreëerd.
De creatieve oplossingsvaardigheid van de decorateurs is verbluffend, maar het plaatje van quasi kristallijne structuren dat Lu & Steinhard voorhielden blijft niet overeind.
Gelukkig blijft de creatieve rijkdom van de exploraties van de decoratieve mogelijkheden overeind.
Lees dus zeker het artikel van Cromwell en blijf je verbazen door de echte patronen!

- Binnen de grote, tienpuntige ster vinden we een krans van... achtpuntige sterren.
- De oranje sterren op de hoekpunten van de grote tienpuntige ster komen allesbehalve mooi uit.
- Kijk je naar de opvulling van met de zeshoeken rond de grote tienpuntige ster, dan merk je dat er heel pragmatisch opgevuld. Zo staat er centraal, omgeven door drie 5-puntige sterren en een strik, een ongewone, witte 8-hoekige vorm die niet thuishoort in het vijfvoudig systeem.