Rotación y simetría en el plano
Introducción
En este ejemplo se representa la funcionalidad de las transformaciones lineales de rotación y simetría.
En el panel derecho se bosquejan las definicones y un funcionamiento básico. Se recomienda usar esto como punto de partida para experimentar.
Definiendo matrices:
Para definir una matriz, debe escribirse por filas, de la siguente forma: M={{1, 2}, {3, 4}}
Definiendo vectores (de ):
Escribirlos entre paréntesis: e1=(1,0)
Producto matricial y producto matriz*vector:
El producto matricial puede realizarse comodamente de la forma A=B*C.
Ahora, en cuanto al producto matriz-vector, si bien puede realizarse de la forma w=A*v, esto se grafica como un punto y no como una flechita en el plano.
Para mostrar el resultado como flecha, se recomienda la sintaxis: w=AplicaMatriz(A,v)
Efecto de la matriz R
La matriz R define una rotación sobre el origen, de un ángulo
Puede mover el ángulo en el deslizador y ver la imagen de los vectores y a travez de la transformación
Efecto de la matriz R
Análisis de la matriz S
La matriz R es claramente una rotación. Se puede interpretar el significado geométrico de S haciendo la siguiente descomposición:
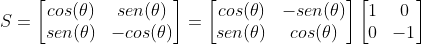Donde se puede notar que:
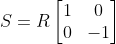Por comodidad vamos a definir:
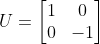Como la transformación lineal correspondiente se puede asociar de la forma significa que, geométricamente, debemos aplicar la transformación U y a la imagen obtenida, rotarla con S.
Se puede observar que U es una reflexión en la dirección del vector e2:
Por otro lado, se puede observar que la transformación compuesta refleja los vectores en una dirección que varía con θ. Se grafica el "espejo" para observar dicho efecto.
Sabiendo este comportamiento de antemano, se puede hallar "facilmente" el vector director de la recta, como: S(x)+x (dibujar el paralelogramo para convencerse). (Esto vale para cualquier reflexion o proyección ¡es importante! Analizalo un toque, siempre la podes reconstruir facilmente teniendo unos pocos vectores y su imagen).
Efecto de la matriz S
Composición de dos rotaciones
A continuación, se compone una rotación de un ángulo con una de un ángulo
Combinación de Rotaciones Ra y Rb
Revisiones
Version 2.1 (2020/06/11)
- Agregada recta espejo de la simetría. ¡Gracias Ale!
Versión 2 (2020/06/11)
- Mejorada la organización
Versión 1.1 (2020/05/27)
- Arreglado error al escribir la matrices R. ¡Gracias Moni!
Version 1 (2020/05/25)
- Creado
Licencia de uso
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.