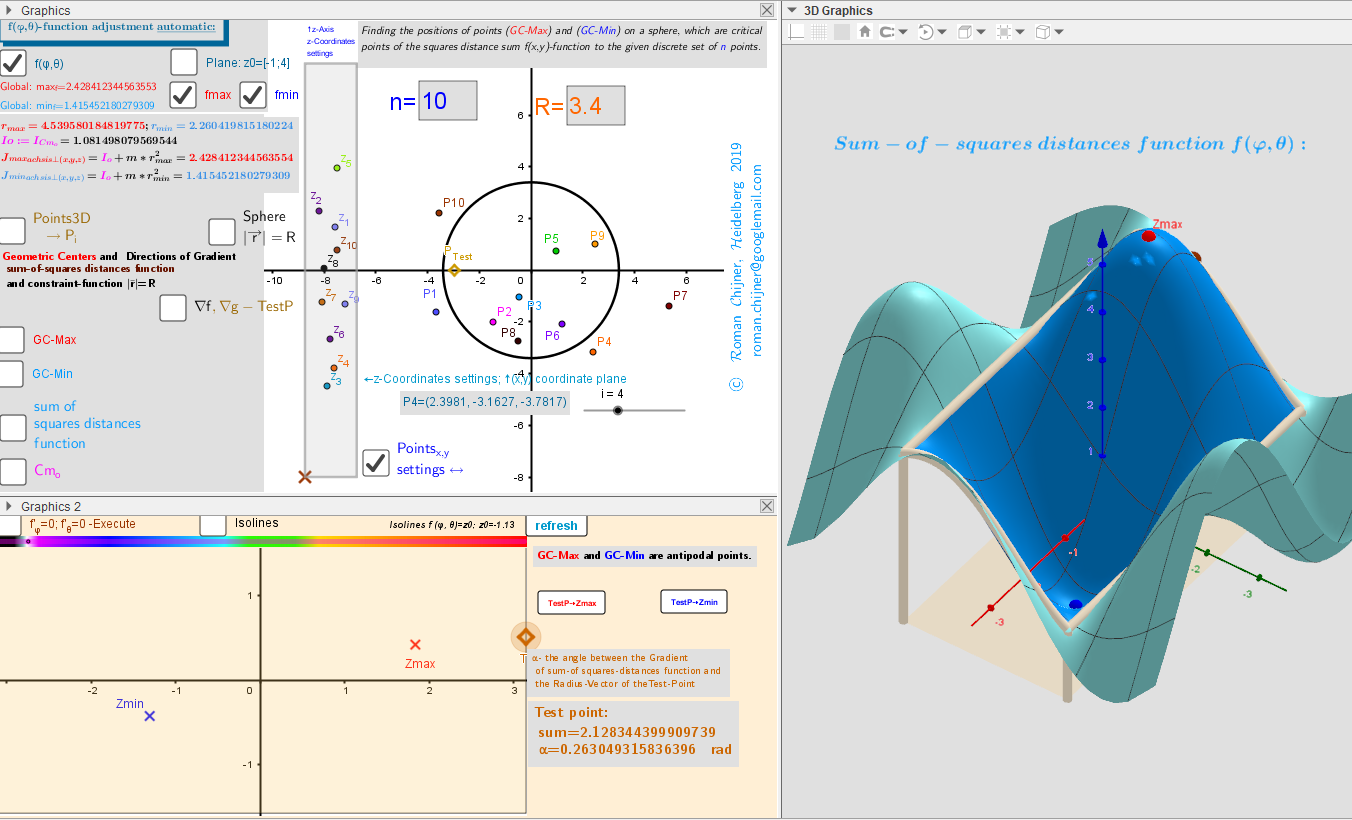
Finding critical points (on a sphere) of a function of sum of the squares of the distances - for n points in ℝ³

Let Pi=(x_i,y_i,z_i) n moving points in ℝ³ (lP:={P1,P2,...,Pn}). I want to find the points P=(x,y,z) on the surface of the sphere -S (radius R) that are critical (relative min/max or saddle points at (x,y,z)) of a function of sum of squares of the distances to the given points Pi. Critical points can be found using Lagrange multipliersas finding the Extreme values of the function f(x,y,z):=-sum of the squares of the distances to the points Pi, subject to a constraining equation g(x,y,z):=x²+y²+z²-R²=0 - points P=(x,y,z)∈S. There is a system of equations: ∇f(x,y,z)= λ∇g(x,y,z). A local optimum occurs when ∇f(x,y,z) and ∇g(x,y,z) are parallel, and so ∇f is some multiple of ∇g. The condition that ∇f is parallel to ∇g either means ∇f = λ∇g or ∇f = 0 or ∇g = 0. The case ∇f = 0 can be included in the Lagrange equation case with λ =0. If we substitute the variable z=R cos(θ), then we will have a two-variable function f(φ,θ) over a rectangular region: - π ≤φ≤ π; -π/2≤θ≤π/2. The solution of the system of equations can be found as the intersection points of the corresponding implicit functions. The point P=(x,y,z) that minimize the sum of the squares of the distances to the points P_iis the geometric center (gravity center, barycenter, center of mass, centroid) GC: Cm=-its coordinates are the averages of the coordinates of the points from set lP. https://en.wikipedia.org/wiki/Center_of_mass It can be shown that in this problem there are only two critical points P=(x,y,z)∈S: one corresponds to the global maximum, the other- to the global minimum. 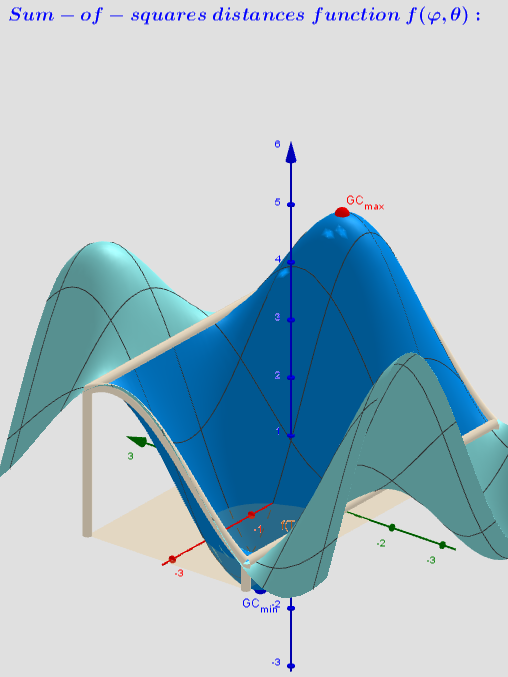Their coordinates have explicit formulas: GC_min= R UnitVector(Sum(lP)) and GC_max= - R UnitVector(Sum(lP)) -two Critical points: regardless of the number of moving particles, the number of extreme points-geometric centers on the sphere is always two: 2 antipodal points on the sphere. These points can also be found using the Steiner theorem. Visually observed and explore these solutions at different positions of the points from set lP you can in applet. Description is in https://www.geogebra.org/m/nge6gawt

Distribution of points P[sub]i[/sub], [color=#ff00ff]Cm[/color], [color=#ff0000]GC[sub]max[/sub][/color] and [color=#0000ff]GC[/color][sub][color=#0000ff]min[/color] [/sub]on a sphere. Vectors ∇f and ∇g at these points. — Distribution of points P_i, Cm, GC_max and GC_minon a sphere. Vectors ∇f and ∇g at these points.

Only Two intersection points of implicit functions -solutions of the Lagrange equation: [color=#0000ff]GC[sub]min[/sub][/color] and [color=#ff0000]GC[sub]max[/sub][/color]. — Only Two intersection points of implicit functions -solutions of the Lagrange equation: GC_min and GC_max.

Isolines around points: [color=#0000ff]Z[sub]min[/sub][/color] and [color=#ff0000]Z[sub]max[/sub][/color]. — Isolines around points: Z_min and Z_max.

Two-variable function f(φ,θ) over a rectangular region: - π ≤φ ≤ π; -π/2≤θ≤π/2.

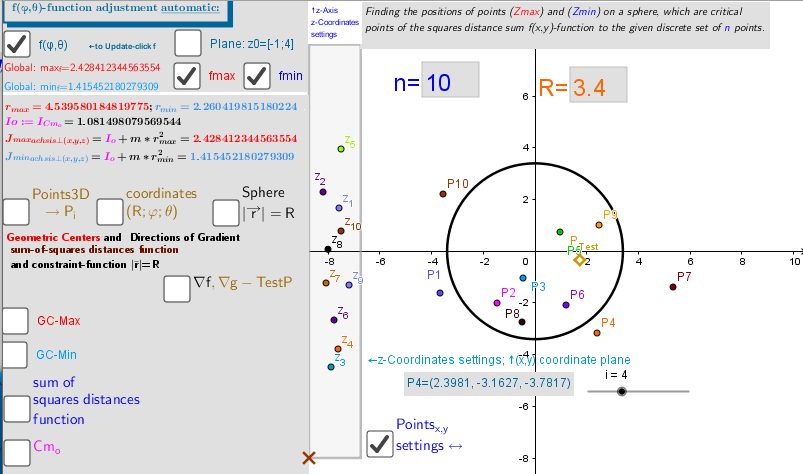
settings plane, equalities from the Steiner theorem

Distribution of Points P[sub]i[/sub]. [color=#783f04]Test Point[/color], GC[color=#ff0000][sub]max[/sub][/color] and [color=#0000ff]GC[sub]min .[/sub][/color] — Distribution of Points P_i. Test Point, GC_max and GC_{min .}

Finding critical points (on a sphere) of a function of sum of the squares of the distances - for n points in ℝ³

New Resources

Discover Resources

Discover Topics