Fatoração de Polinômios
Um polinômio na variável é uma expressão algébrica que envolve apenas as operações adição, subtração e multiplicação entre números e a variável . Por exemplo, é um polinômio pois
Da mesma forma, também é um polinômio pois
Já , e não são polinômios, pois nessas expressões aparecem operações diferentes da adição, subtração e multiplicação. Mas note que é um polinômio, pois e são apenas maneiras de representarmos certos números reais ( e ).
Podemos pensar um polinômio como uma máquina que pega um certo número e calcula um certo número usando apenas as operações de adição, subtração e multiplicação. Por exemplo, se , temos que , , etc.
Forma Expandida e Forma Fatorada
Considere os polinômios e que mencionamos anteriormente. Desenvolvendo , temos que
ou seja, e são duas "máquinas" que calculam sempre o mesmo resultado para as mesmas entradas. Ou de outra forma, são representações diferentes do mesmo polinômio. Dizemos que está na forma expandida e que está na forma fatorada.
É muito fácil passar um polinômio da forma fatorada para a forma expandida, basta aplicar a propriedade distributiva da multiplicação com relação à adição, por exemplo,
O grau de um polinômio em é o valor do maior expoente de na forma expandida. Por exemplo, é um polinômio de grau 1 (ou linear), é um polinômio de grau 2 (ou quadrático), é um polinômio de grau 3 (ou cúbico) etc.
Mas o problema inverso, pegar um polinômio na forma expandida e fatorá-lo como um produto de dois polinômios de grau menor parece ser mais difícil. Na verdade, não está claro que sempre podemos fatorar um polinômio. Por exemplo, como fatorar
?
Teorema Fundamental da Álgebra
Temos uma boa e uma má notícia. A boa notícia é que qualquer polinômio (não constante) pode ser fatorado como um produto de fatores lineares, resultado conhecido como Teorema Fundamental da Álgebra. Alguns desses fatores podem envolver números complexos, mas isso não é um problema. Por exemplo, usando o fato que o número imaginário puro satisfaz a propriedade , temos que
,
Portanto a forma fatorada do polinômio é . A má notícia é que pode ser muito difícil obter a fatoração do polinômio, ou seja, o Teorema Fundamental da Álgebra diz que a fatoração é possível, mas não que seja fácil. A seguir veremos algumas técnicas que nos ajudam a fatorar um polinômio.Equações e Inequações Polinomiais
Mas antes de tratar dessas técnicas, por que mesmo estamos preocupados com esse problema de fatorar polinômios? A resposta vem da junção de dois fatos:
- muitos problemas recaem na solução de equações ou inequações polinomiais;
- equações ou inequações polinomiais são mais facilmente resolvidas na forma fatorada.
,
portanto na forma fatorada a equação fica assim: Agora fica muito mais fácil descobrir as soluções da equação, pois quando é que o produto de dois números é zero? Apenas se ou . Assim, onde o símbolo significa se, e somente se, ou é equivalente a, ou seja, se é uma solução de , então ou e e são de fato soluções da equação. Da mesma forma, veremos que inequações polinomiais, ou seja, inequações da forma ou com polinômio são mais facilmente resolvidas se está na forma fatorada.Fatoração através de Manipulações Algébricas
Podemos fatorar um polinômio através do uso de identidades e manipulações algébricas. Vejamos alguns exemplos:
Examplo: Fatore .
Examplo: Fatore .
Esse polinômio parece muito com a expansão de , vamos forçar para que ela apareça:
.
Agora temos uma diferença de cubos:,
donde concluímos que.
Examplo: Fatore . Fazendo , temos que Portanto.
Mas é uma diferença de cubos, assim.
Fatoração e Raízes
Um número é uma raiz de um polinômio se . É claro que se , então é uma raiz de . Mas usando o algoritmo de divisão de polinômios, que é bem semelhante ao algoritmo de divisão com resto de números inteiros, é possível mostrar o inverso, pois como pelo algoritmo da divisão, se é uma raiz de então . Assim, é uma raiz de se, e somente se, o resto da divisão de por é zero. Portanto, se de alguma maneira, mesmo que por tentativa e erro, descobrirmos que , podemos dividir por para descobrir o outro fator .
Por exemplo, considere o polinômio
É imediato ver que . Portanto para um certo fator . Para descobri-lo, efetuamos o algoritmo da divisão de polinômios:
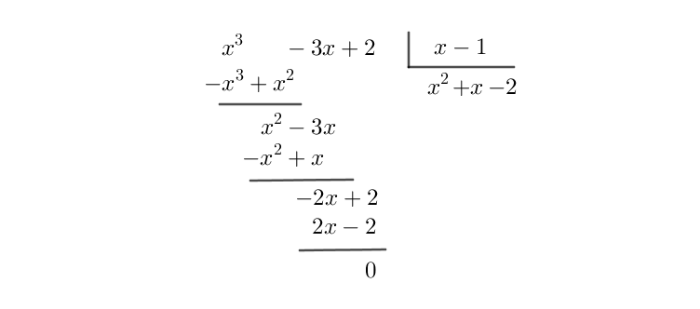
Portanto,
Como claramente , chegamos a fatoração completa
Dispositivo de Briot-Ruffini
Existe um modo mais prático de efetuar a divisão de um polinômio por um polinômio linear conhecido como dispositivo de Briot-Ruffini. Ele contém as mesmas contas do algoritmo de divisão, só que efetuadas de forma resumida. No caso do exemplo acima, temos o seguinte:
A figura acima é manipulável, experimente mover os controles. A ideia é que se
então, para calcular e o resto , fazemos
Para um polinômio de grau , a esquema é o mesmo.
Estratégias para Encontrar as Raízes
Existem algumas estratégias para encontrar as raízes de uma equação polinomial. Vamos comentar apenas uma. Suponha que seja um polinômio com coeficientes inteiros e cujo coeficiente principal (o coeficiente que multiplica o termo de maior grau) seja igual a . Por exemplo, para grau ,
com . Se possui uma raiz inteira , temos que
portanto
ou seja, necessariamente é um divisor de (já que é inteiro). Assim, a única chance de possuir uma raiz inteira é se está entre os divisores de . Note que esse resultado não diz que as raízes de são os divisores de . Vamos aplicar essa estratégia em um exemplo. Exemplo: Fatore . Os divisores de são ou . Vamos verificar se algum desses valores é uma raiz de : Portanto e são as únicas raízes inteiras de . Note que avaliamos para todos os divisores, mas na prática podemos parar na primeira raiz que encontrarmos. Aplicando Briot-Ruffini duas vezes (tente você mesmo!), concluímos que . Se for necessário, podemos fatorar completamente calculando as raízes de através da fórmula de Bhaskara.
Exercícios
Fatore os seguintes polinômios: