Nadir Divanbegi Khanagah - gp
De Nadir Divangegi Khanagah (1619-1623) diende als bijeenkomstplaats voor Sufi's en ligt aan de westkant van het Lyab-i Hauz-geheel, centraal in Bukhara. Het werd gebouwd door vizir Nadir Divan-begi, nonkel van Imam Quli Khan, de heerser van Bukhara in de periode1611-41.
De khanaqah is een van een trio gebouwen, opgetrokken rond een vijver en dat geeft het geheel zijn naam: Lyab-i Hauz betekent "bij de vijver" in het Perzisch.
Het lijnenpatroon op het zwik bovenaan op de iwan is opgebouwd vanuit twaalfhoeken, negenhoeken en strikken, net zoals het zwik van de oostelijke iwan van de Kalon moskee.

Het verschil tussen beide is de schikking van het patroon op het zwik (zie figuur 1).
Het patroon op de Kalon moskee werd hier lichtjes uitvergroot.
- Waar het patroon op de Kalon moskee tussen de twaalfhoeken in de bovenhoeken twee halve twaalfhoeken geplaatst werden, staat er nu nog slechts één halve.
- Langs de onderrand staan nu in zowel in de hoeken als centraal negenhoeken.
- Het resultaat is dat het patroon op de Nadir Divanbegi Khanagah minder maar grotere sterfiguren bevat.

een vlieger in de strikken
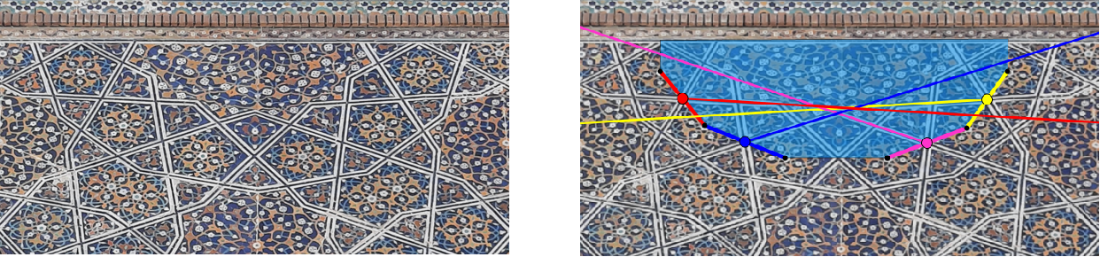
Figuur 2: Trek je vanuit een punt van een twaalfpuntige ster de lijnen door, dan lopen die niet door een ander hoekpunt van de ster, m.a.w. in het patroon worden de middens van de zijden van de veelhoeken niet verbonden met het midden van een andere zijde.
De reden is eenvoudig: om in de strikken vliegers te bekomen zonder knik in de overgangen tussen twaalfhoek en strik. Daarom wordt de methode om sterren te vormen door middens met middens te verbinden, verlaten zodat doorlopende lijnen in de overgangen wel vliegers opleveren.
het patroon
De oplossing om met doorgaande lijnen wel een vlieger te bekomen is simpel: keer de logica om.
Vertrek niet van lijnen in de twaalfhoek, maar van de negenhoek en creëer doorlopende lijnen om de tophoek van de twaalfpuntige ster te bepalen.
- Bepaal de middenpunten van de aangrenzende zijden van een twaalfhoek en twee negenhoeken.
- Construeer in de twee negenhoeken een lijn die bij een 9-3 ster hoort.
- Teken de rechten door het middelpunt van de zijde op de twaalfhoek en de middelpunten van de zijden op de negenhoeken en bepaal voor beide rechten het snijpunt met de overeenkomstige vierde zijde in de twaalfhoek.
- Hiermee is de tophoek van de 12-puntige ster bepaald. Je kunt nu in de negenhoeken een 9-3 ster construeren en in de twaalfhoeken een ster met tophoeken zo dat doorlopende lijnen in de strik een vlieger bepalen.