Posizione reciproca tra retta e parabola
In questo capitolo studiamo la posizione reciproca tra una parabola ed una retta. Disegnando alcuni esempi ti puoi rendere conto che una retta può incontrare una retta:
- in due punti (in questo caso si parla di retta secante, ovvero che taglia la parabola)
- in un solo punto (retta tangente, ovvero che tocca la parabola)
- in nessun punto (retta esterna alla parabola, cioè che non la incontra)
Nell'ultima parte dell'animazione abbiamo visto che DI TUTTE LE RETTE PARALLELE alla retta , quella TANGENTE alla parabola dell'esercizio ha , e quindi la retta cercata è .
Terminiamo l'esercizio trovando il punto di tangenza in cui parabola e retta si trovano. Il metodo più naturale per farlo è mettere a sistema la retta appena trovata e la parabola
Fai i conti e trova le coordinate e del punto in comune, come mostrato nella prima parte della presentazione.
UN'ALTERNATIVA RAPIDA (DA CAPIRE BENE)
C'è un metodo più rapido. Mentre hai fatto i conti forse hai notato che hai ripetuto esattamente molti dei passaggi descritti nella presentazione, semplicemente dove nella presentazione c'era scritto tu avevi il valore "giusto" 2. Ma i conti erano gli stessi.
Possiamo quindi sfruttare i conti già fatti, arrivare alla fine e copiare l'equazione associata, quella che ci permette di trovare i valori dei punti in comune, sostituendovi 2 al posto di :
Se controlli ora i conti che hai fatto sul quaderno, vedrai che è la stessa equazione che hai trovato tu... facendo ben più passaggi. Il risultato è ovviamente lo stesso: , che sostituito nella retta ci da anche l'altra coordinata, .
Quindi se abbiamo già costruito ed elaborato il sistema per trovare la condizione di tangenza, possiamo sfruttare il lavoro fatto anche per ottenere le coordinate del punto.
CONFRONTIAMO I RISULTATI NEL CASO DI TANGENZA, SECANZA ED ESTERNALITÀ
Se osservi con attenzione i risultati ottenuti nell'ultima parte dell'animazione qui sopra, noterai che il risultato ottenuto per la condizione di tangenza (cioè q=2) è direttamente collegato alle rette secanti, che in questo caso hanno q>2, e quelle esterne, cioè q<2 (NOTA: questi risultati nell'animazione non sono ottenuti da calcoli, ma puoi verificarli cambiando con l'interruttore il valore di q e muovendo la retta).
Questo perché le tre condizioni sono sempre legate al DELTA dell'equazione associata al sistema, semplicemente di volta in volta poniamo questo stesso DELTA
- maggiore di zero se vogliamo due soluzioni, quindi la secanza
- uguale a zero per avere una sola soluzione in comune, quindi tangenza
- minore di zero se vogliamo che retta e parabola NON si incontrino, cioè esternalità
Terminiamo ora l'esercizio dell'animazione.
Abbiamo trovato che le rette che passano per il punto hanno tutte la forma - scegliendo un valore per trovo una delle rette. Imponendo la condizione (secante - DUE punti in comune) ho trovato che deve essere . Il risultato finale è quindi che le rette passanti per hanno la forma
con
In questo caso questo è l'unico modo per descrivere TUTTE le rette richieste: non possiamo elencarle una ad una, sono infinite! allo stesso modo non possiamo trovare i punti di contatto, perché ognuna avrà i suoi due (potremmo fare i calcoli per una retta di esempio, ad esempio per , che è uno dei valori che vanno bene).
Proviamo a trovare le rette che passano sempre per , ma che sono TANGENTI alla parabola. Dobbiamo mettere a sistema le rette, che sono sempre quelle, con la parabola
mi rendo conto che sto ripetendo gli stessi identici passaggi di prima! I calcoli saranno gli stessi, fino a quando arrivo alla equazione associata:
È a questo punto che il procedimento cambia! Non devo più imporre che (due punti-soluzione, secanza) ma che (un solo punto-soluzione in comune: tangenza):
risolvendo trovo i due valori e .
NOTA: sono gli stessi risultati di prima! infatti per applicare il metodo della parabola ho dovuto risolvere l'equazione associata alla disequazione!
In questo caso ci sono solo due valori "giusti", quindi possiamo sostituirli per trovare le rette corrispondenti ed anche i relativi punti di tangenza.
Per trovare le due rette sostituisco ora uno alla volta i valori trovati nella retta generica:
Per trovare i due punti di tangenza in cui le due rette toccano la parabola, devo prenderle una alla volta e metterle a sistema con la parabola. Fallo sul tuo quaderno poi continua a leggere.
Oppure posso accorgermi che ancora una volta i conti del sistema sono sempre gli stessi - semplicemente una volta al posto di ci sarà , e la seconda volta ci sarà . Allora posso ripartire direttamente dall'equazione associata, in cui la prima volta sostituisco , e la seconda volta sostituirò .
Vediamo il primo caso con
Questa equazione ha una sola soluzione (doppia), cioè . Puoi controllare sul tuo quaderno che facendo tutto il procedimento avevi trovato esattamente gli stessi risultati. Per trovare la del punto di tangenza andiamo a sostituire nella retta :
Il punto in cui la retta incontra la parabola ha coordinate . Allo stesso modo si trova il punto di tangenza della retta .
FACCIAMO IL PUNTO
Dalle due animazioni dovrebbero essere chiare le operazioni da seguire. Proviamo a riassumerle nel seguente grafico (puoi scaricarlo a questo indirizzo: https://drive.google.com/file/d/1FHkbLEpyq9YqSQ2ptI7J65Xk_TWMvW6s/view?usp=sharing)
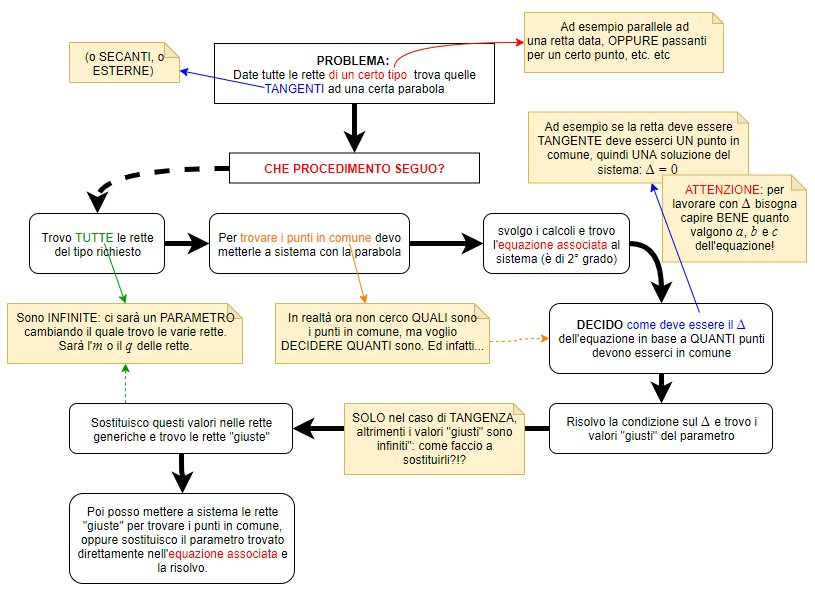
UN ALTRO MODO PER TROVARE LE RETTE PASSANTE PER UN PUNTO DATO
Aggiungiamo qui un modo alternativo per determinare le rette passanti per un certo punto . Non è essenziale saperlo, ma UNA VOLTA CHE L'ABBIAMO CAPITO può renderci più veloci i conti.
Consideriamo l'equazione
dove e sono le coordinate dei punti per cui deve passare la retta. è il coefficiente angolare e dandogli un valore qualsiasi otterremo una rette che passano per A.
Notiamo infatti che qualsiasi sia il valore di , l'equazione è soddisfatta dal punto A, e quindi la retta ci passa. Infatti sostituendo le coordinate del punto al posto di ed otteniamo
cioè l'equazione è soddisfatta da qualsiasi m.
Puoi vedere la cosa anche con un esempio concreto. Ad esempio consideriamo un punto qualsiasi : applicando questa idea otteniamo le rette
Puoi vedere facilmente che sostituendo le coordinate di A l'equazione è soddisfatta per qualsiasi m. Quindi tutte le rette fatte così, qualsiasi sia il valore di m, passano per il punto A. Sviluppando i calcoli otteniamo
Abbiamo ottenuto la conferma che m è il coefficiente angolare di queste rette, infatti è il valore per cui è moltiplicata la x nella forma esplicita, come da definizione.
Trovi altre spiegazioni e chiarimenti a proposito di questa formula nella seconda animazione ("ESEMPIO DI TRASLAZIONE: RETTE PER UN PUNTO") di questa pagina: https://www.geogebra.org/m/bENRgkEw#material/HPG8sKca