Hurdling the Bar
How do you hurdle the bar?

OBJECTIVE: To learn how to convert repeating decimals to fractions
In a previous lesson, you learned how to convert FRACTIONS to DECIMALS by dividing the numerator by the denominator.
Getting to the Point: https://www.geogebra.org/m/wz32mw3y
In that lesson, you discovered that doing so sometimes leads to TERMINATING DECIMALS, but at other times, you get REPEATING DECIMALS. In another lesson, you learned how to convert TERMINATING DECIMALS to FRACTIONS.
Missing the Point: https://www.geogebra.org/m/vjjpprfm
In this lesson, you're going to learn how to convert REPEATING DECIMALS to FRACTIONS.
Here are the steps:
Step 1: Separate the integral part and the decimal part of the number.
Step 2: Convert the decimal part into a PROPER FRACTION as follows:
(1) Write the numerator as the difference between number formed by the decimal digits and the number formed by the nonrepeating digits.
(2) Write the denominator as a series of 9's and 0's, representing each repeating digit as 9 and each nonrepeating digit as 0.
(3) Reduce the resulting fraction to lowest terms.
Step 3. Write the integral part and the fraction as a mixed number.
Examples:



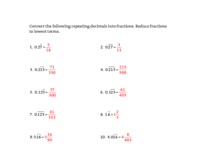
Below is a set of problems involving converting repeating decimals to fractions.
Converting Repeating Decimals to Fractions
ANSWER BOX:
Check your answers below.
Converting Repeating Decimals to Fractions_Answer Key
In this lesson, you learned how to convert repeating decimals into fractions.
In future lessons, you'll learn more about decimals and fractions. Hope you had FUN today!