Melukis Grafik Fungsi Kuadrat
Tujuan Pembelajaran :
- Peserta didik dapat menentukan fungsi kuadrat
- Peserta didik dapat melukis fungsi kuadrat
Pengertian Fungsi Kuadrat
Fungsi kuadrat adalah sebuah fungsi polinom yang memiliki peubah/variabel dengan pangkat tertingginya adalah 2 (dua).
Fungsi kuadrat adalah fungsi yang berbentuk f(x) = ax2 + bx + c untuk a dan b sebagai koefisien dan c adalah konstanta dengan a, b, dan c adalah bilangan riil dan a ≠ 0.
Fungsi kuadrat dapat digambarkan ke dalam koordinat kartesius dengan y = ax2 + bx + c dimana x sebagai variabel bebas dan y adalah variabel terikat berbentuk seperti parabola sehingga sering disebut sebagai grafik parabola.
Jenis-Jenis Fungsi Kuadrat 1. Jika pada y = ax2 + bx + c nilai b dan c adalah 0,
- maka fungsi kuadrat menjadi : y = ax2
- grafik pada fungsi ini simetris pada x = 0
- dan memiliki nilai puncak di titik (0,0)
- maka fungsi kuadrat akan berbentuk: y = ax2 + c
- grafik pada fungsi ini simetris pada x = 0 dan memiliki titik puncak di (0,c)
- maka fungsi kuadrat menjadi: y = a(x – h)2 + k
- Menentukan sumbu simetri: x = – b/2a
- Menentukan titik potong kurva dengan sumbu x: misalkan y = 0, maka ax2 + bx + c = 0
- Menentukan titik potong dengan sumbu y: misalkan x = 0, maka y = c
- Menentukan titik puncak: y = - D/4a
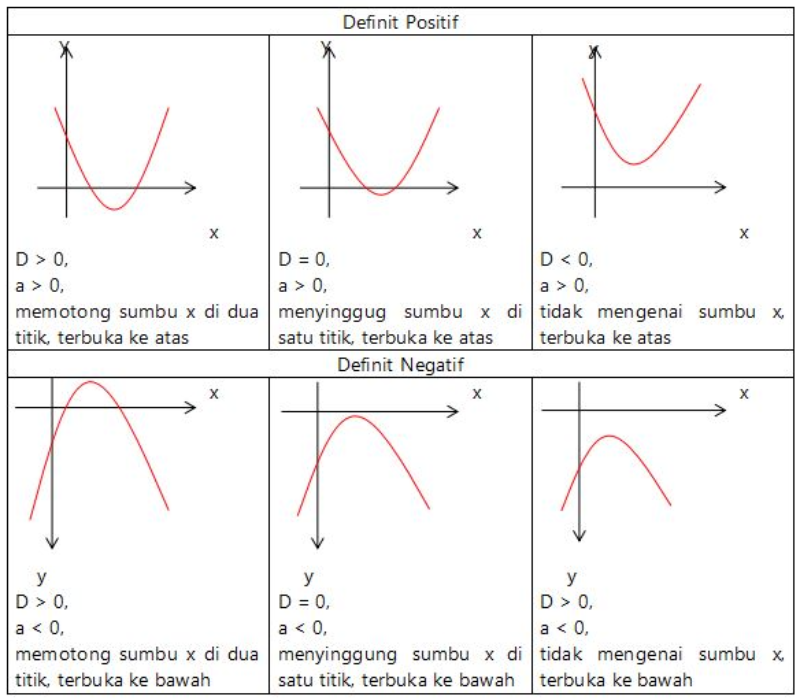
- Jika a > 0 maka parabola terbuka ke atas jika sebaliknya maka parabola terbuka ke bawah.
- Kemudian pada fungsi kuadrat terdapat istilah diskriminan yang memiliki bentuk:
- D = b2 – 4ac
- Jika D > 0 maka fungsi kuadrat memiliki 2 akar yang berbeda dan memotong di dua titik.
- Jika D = 0 maka fungsi kuadrat memiliki 2 akar yang sama, sehingga kurva hanya akan menyinggung sumbu x di satu titik.
- Jika D < 0 maka kurva tidak menyentuh sumbu x sama sekali.
Rumus Fungsi Kuadrat
Latihan A
LATIHAN B
Tentukan nilai maksimum dari fungsi y = x2 – x – 6.
Koordinat titik balik grafik fungsi kuadrat y = 2x2 – 4x + 5 adalah ...
Marca todas las que correspondan
- A
- B
- C
- D
- E