ENEM 2018/2010: Classificação de Triângulos e Cálculo de Área
Neste material vamos classificar os tipos de triângulos e abordar de maneira objetiva cinco formas de se calcular a Área de Triângulos.
1. Classificação dos triângulos quanto aos lados: Podemos classificar um triângulo de acordo com a medida de seus lados. Temos três possíveis combinações em relação ao tamanho dos lados: ou todos os lados são iguais, ou dois lados são iguais e um diferente, ou todos os lados são diferentes. 2. Classificação dos triângulos quanto aos ângulo: Temos três possíveis combinações em relação ao tamanho dos seus ângulos internos: todos os seus ângulos internos menores que 90°; um de seus ângulos internos é um ângulo de 90°; e um dos seus ângulos internos com medida maior que 90° e menor que 180°
CONSTRUÇÃO 1: Manipule os controles deslizantes para analisar e classificar os tipos de triângulos.
Aplicação no ENEM - 2018
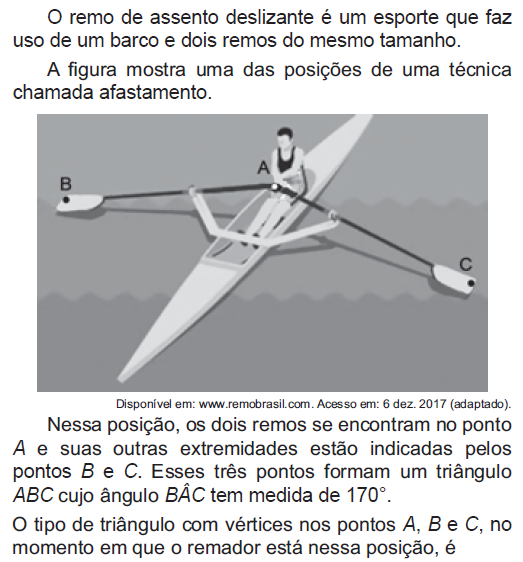
Após o estudo da classificação dos triângulos, responda.
Tire sua dúvida, caso exista, assistindo à videoaula.
Área do triângulo em função dos lados e suas respectivas alturas.
Para calcularmos a área do triângulo, devemos multiplicar a base pela altura, dividindo por 2. Assim , onde b é o valor da base e h é a altura do triângulo.
CONSTRUÇÃO 2: Movimentando o ponto C, sobre a reta "r" que é paralela a base (AB) do triângulo, nem o comprimento da base nem a altura (distância entre as paralelas) é alterada, portanto a área permanece a mesma, apesar dos triângulos serem diferentes.
Movimentando os pontos A e B pertencentes ao segmento AB. Durante a atividade, você pode duplicar o separador de abas para manusear de forma mais prática a construção do GeoGebra. (clique com o botão direito do mouse na aba da atividade e selecione com o
O que ocorre com a área do triângulo ABC, quando aumentamos ou diminuímos apenas o segmento AB, através da movimentação dos pontos A ou B sobre a reta s, deixando a altura constante?
Movimentando a posição da reta "r" e deixando fixo o tamanho do segmento AB.
Movimentando a posição da reta "r" em relação à base AB do triângulo e deixando fixo o tamanho do segmento AB, o que ocorre com a área do triângulo ABC?
CONSTRUÇÃO 3: Manipule o controle deslizante para comparar a área do triângulo ABC com a área do paralelogramo ABE'E,
Exercício de fixação.
A base de um triângulo mede 72 cm e sua altura, em centímetros, é h. Se a base for aumentada em 48 cm e a altura em 32, obtém-se um novo triângulo, cuja a área é o triplo da área do primeiro. Qual é o valor da altura h?
Assista á videoaula e tire sua dúvida.
CONSTRUÇÃO 4: Manuseando os pontos A, B e C, obtemos a área do triângulo (ABC) em função dos lados “b” e “c” e o ângulo α, compreendido entre eles.
Como calcular a área do triângulo, dispondo do tamanho de dois lados e do ângulo compreendido entre eles.
Na construção anterior, temos os seguintes triângulos:
- é o triângulo formados pelos pontos A, B e C;
- é o triângulo formados pelos pontos B, C e D (retângulo em D);
- é o triângulo formados pelos pontos A, B e D (retângulo em D).
Exercício para fixar os conceitos estudados anteriormente.

A videoaula contém uma solução para o problema anterior.
CONSTRUÇÃO 5: Área do triângulo, dispondo do raio da circunferência inscrita no triângulo e do semiperímetro ou do tamanho dos lados do triangulo(a, b e c).
Na construção 5, temos duas formas de calcular a área do triângulo ABC, Movimente qualquer um dos vértices do triângulo ABC e dispondo de uma calculadora, determine a raiz quadrado do valor de (Fórmula de Heron). Comparando os valores de e , o que ocorre? Como devemos decidir qual das fórmulas devemos usar?
Exercícios de fixação.
Determine a medida do raio de um círculo inscrito em um triângulo isósceles de lados 10 cm, 10 cm e 12 cm.
Acompanhe a videoaula e tire sua dúvida.
Exercício de fixação.
Os lados de um triângulo medem 17 m, 15 m e 8 m. determine a sua menor altura.
CONSTRUÇÃO 6: Área do triângulo inscrito na circunferência.
Analisando a construção 6.
Alterando a posição de qualquer um dos pontos A, B ou C, obtemos um novo triângulo inscrito, você já percebeu que . Em qual situação devemos usar ?
Qual é a definição de mediatriz de um segmento?
Qual é o nome do ponto determinado pela intersecção das mediatrizes de um triângulo?
Exercício de fixação.
Determine a medida do raio de um círculo circunscrito em um triângulo isósceles de lados 10 cm, 10 cm e 12 cm.
Caso tenha dúvida, assista à videoaula.
ENEM 2010
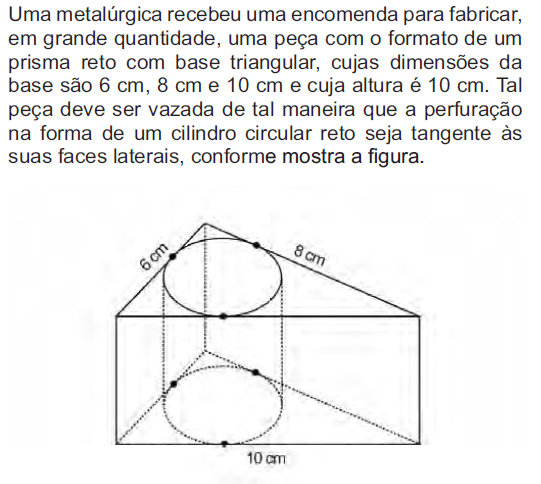
O raio da perfuração da peça é igual a: