Folding Rectangle Puzzle
My student Leo K. found and emailed a graphic to me in late 2021, inspiring this puzzle.
Start with a letter-sized (USA) piece of paper, 8.5" x 11".
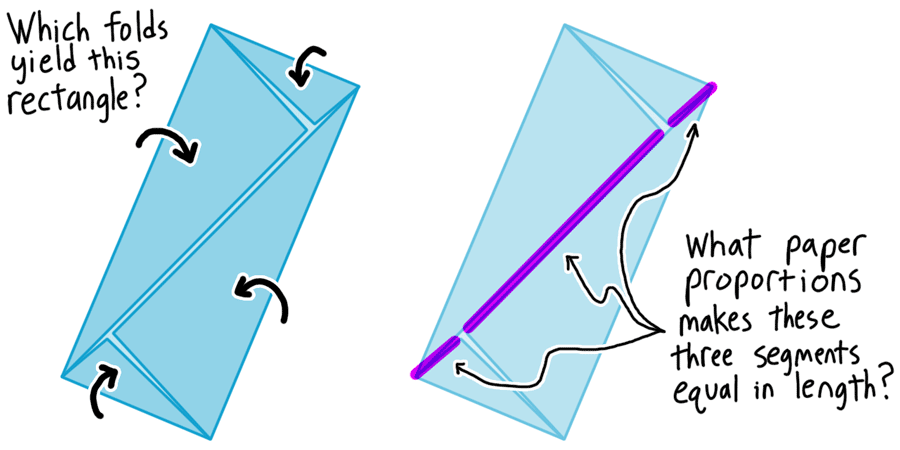
Fold along line BC. Repeat the fold symmetrically on the opposite corner. (Drag the GeoGebra slider halfway to simulate this.) Then fold the other two corners of the original rectangle along the angle bisectors that appear in the GeoGebra construction. (Drag the slider the rest of the way to simulate.)
Drag points A, B, and C to change the size of the paper and/or the position of the folds. If the "paper" becomes unshaded, that means that the creases will intersect each other... and that's not what we want for the sake of this puzzle.
Puzzle:
- Where must points B and C be positioned along the edges of the letter-sized paper such that these steps yield a rectangle that is exactly two layers of paper thick everywhere?
- Find a general formula for part (I) that works for any size of paper.
- Instead of letter-sized paper, what must be the proportions of the paper such that the diagonal of the resulting rectangle is trisected by the original paper edges?
- If you want the resulting rectangle to be of a specified size, find a general formula for the size of the paper that you must start with.