群にも相似と合同がある?
1.ほぼ同じとぴったり同じ
このワークシートはMath by Codeの一部です。
<イメージトレーニング>
厳密に考える前にイメージトレーニングをしてみよう。
2つの図形が似てる場合は相似があるね。形が同じだから。
さらに、図形の辺の長さまで同じ相似形は合同といったね。
しくみ、つまり、2つの群の形、つながり方が同じなのが準同型homo-morphism(群の相似)で、
さらに、群のサイズ、位数とまで同じで、ぴったり重ねられるのが同型iso-morphism(群の合同)
語源的にも、morphはshape、形のことで、
homoはsimilar、つまり似ているだけだから、相似と同じ。
isoはsame、equal、つまりぴったり等しいから、合同。
ついでに、対称図形のように自分に重ねられる自己同型auto-morphism(対称性のある群)がある。
三角形ABCと三角形DEFが合同なとき、△ABC≡△DEFとかいた。
群Gと群Hが同型なとき、G≅Hとかく。
同型では単位元と単位元が1対1に対応し、逆元は逆元に対応する。また、各要素の位数も維持される。だから、同型っていうのは、同じ構造の別名、エリアスという感じだ。
<余りと準同型の例>
たとえば、
群G1=<N,+>
領域N:整数のあつまり。
領域のサイズ:無限
演算+:2数の和。(N, N)->N
単位元は0,xの逆元は-x。
群G2=<Z4,⊕>
領域Z4:{0,1,2,3}
領域のサイズ:4
演算⊕:2数の和を4で割った余り。(Z4,Z4)->Z4
単位元は0, xの逆元は-x(具体的には0⊕0=0,1⊕3=3⊕1=0, 2⊕2=0)
写像f:G1→G2について、
N→Z4でNを4で割った余りを求める。
たとえば、f(12+13)=f(25)=1 、f(12)⊕f(13)=0⊕1=1から、f(12+13)=f(12)⊕f(13)
一般に、どんなx、yについてもf(x + y) =f(x)⊕f(y)
演算結果の写像は、写像の演算結果に等しい。
2つの群で、これが言えるときにfを準同型写像という。
三角形の相似でイメージしてみよう。
平面G1にある3点A,B,Cがx、x+y、yで、Bにできる角は演算+できまる。
平面G2にある3点A',B',C'がf(x),f(x)⊕f(y),f(y)で、B'にできる角は演算⊕で決まる。
すると、平面G1の角x+yを写した先f(x+y)がf(x)⊕f(y)に重なるということだね。
写像fが演算による要素のつながり具合、つまり、形を保つ相似な写像といえる。
それが準同型写像だ。
すると、
・f(0)=0 だから、f(単位元)=単位元となる。
・f(x)=y、f(-x)=zとする。f(0)=f(x+(-x))=f(x)⊕f(-x)=y⊕z=0だから、z=-y。つまり、f(逆元)=逆元となる。
2つの領域はちがうが、演算の効果は対応している。まるで、2つの図形の相似のようだ。
<準同型fで大切なこと>
(必要なこと)
・G1で演算した後にfで写しても、fで写した後でG2で演算しても、同一になる。
・fでG1の単位元がG2の単位元にうつる。
準同型なら、f(e)=f(e*e)=f(e)×f(e) となるね。
両辺にf(e)の逆元をかけて、左辺=f(e)-1×f(e)=単位元、右辺=f(e)だから、f(e)=単位元
・fでG1の逆元がG2の逆元にうつる。
準同型なら、f(e)=f(x*x-1)=f(x)×f(x-1)となるね。
両辺にf(x)の逆元をかけて、左辺=逆元、右辺=f(x-1)となるから、f(x-1)=逆元
(なくてもよいこと)
・単射、1対1の写像(別の出発点からfによる行先で同じかぶらない)one-to-one
・全射(上への写像)fの像が写像先の領域を全部の上を覆って向かっている。onto
(部分群にも着目しよう)
2つの群の写像fが準同型のとき、
・G1のfの像f(G1)をImfとかく。imfはG2の部分で、単位元の像もあるから部分群になる。
・fの行先が単位元となるもと,核kernelをf-1(1G2)をkerfとかく。
kerfは、G1の部分で単位元のもとの単位元たちもあるから部分群になる。
・もしも、kerf=1G1ならG1,G2の単位元が1対1対応となるから、fが単射ということだね。
・部分群は部分群にうつる。
部分群の単位元、逆元はfで上述の議論と同様にして、単位元、逆元は単位元、逆元にうつるので、
imf(部分群)は部分群を作るね。
<回転と準同型の例>
領域C4:{1, i, -1,-i}
領域のサイズ:4
演算*:複素数の積。(C4,C4)->C4
単位元は1, xの逆元はx-1
領域 行列R4:{R(0),R(π/2),R(π),R(3/2 π)}
R(k)=R(π/2 *k)={{sin(π/2*k) , -cos(π/2*k)}, {cos(π/2*k), sin(π/2 *k)}}(K=0,1,2,3とおける。)
領域のサイズ:4
演算 @:行列の積。(R,R)->R
単位元はR(0) , R(x)の逆元はR(-x)。
写像 f: i ^k->R(π/2*k)
つまり、この順にf: {1, i, -1,-i}->{R(0),R(π/2),R(π),R(3/2 π)}に移そう。
そうすると、
たとえば、f(i*i)=f(-1)=R(π)、f(i)@f(i)=R(π/2)@R(π/2)=R(π) iの2乗は90度回転の2乗。
一般に、f(x * y) =f(x)@f(y)
積に対応する回転は、対応する回転の積に等しい。
f(1)=R(0)。f(単位元)=単位元
f(x)=y、f(-x)=zとする。f(0)=f(x*(-x))=f(x)@f(-x)=y@z=R(0)だから、z=-y。
つまり、f(逆元)=逆元となる。
領域はちがうけれど、サイズは4で等しい。
要素が1対1対応(単射)で全射、つまり全単射。
つまり、写像が全単射だから、逆向きでも同じく準同型になる。
このように、双方向に準同型になるときは、2つの群は同型といえるし、
写像も同型だ。図形でいうと合同だね。
C4≅R4になるね。
2.準同型を同型にするわり算
<剰余系で、準同型を同型にしよう>
整数全体Nと領域Z4ではサイズがちがいすぎて、同型のはずがない。
そこで、領域Nを写像先と同じサイズの4に分割しよう。
4の倍数、H0=4ZでNを分割する。
H0は4の倍数の集合
H1は4で割って1余る数の集合
H2は4で割って2余る数の集合
H3は4で割って3余る数の集合
領域H4:{H0,H1,H2,H3}
領域のサイズ:4
演算+:2数からとった要素の和が属する集合。(N, N)->N
単位元はH0,Hxの逆元はH-x。(具体的にはH0+H0=H0,H1+H3=H3+H1=H0, H2+H2=H0)
領域Z4:{0,1,2,3}
領域のサイズ:4
演算⊕:2数の和を4で割った余り。(Z4, Z4)->Z4
単位元は0, xの逆元は-x(具体的には0⊕0=1,1⊕3=3⊕1=0, 2⊕2=0)
写像f:H4→Z4でNを4で割った余りを求める。
fは順に{H0,H1,H2,H3}->{0,1,2,3}の対応になる。
これは明らかに同型写像だね!
領域の要素が全単射になれば、準同型+全単射=同型だね。
H4≅Z4だ。
<空間でも同型写像>
領域:線形空間V
演算+: 位置ベクトルは和について閉じているから加法群、線形空間。
写像f:V->V
Vの各要素に対する計算結果でVをVに変換する。
線形代数でも準同型を同型にするために空間を割る方法がある。
<dim>は、線形空間の次元
<Imf>は、線形空間のfによる行先、像としての線形空間V
<Kerf>は、f-1(0)、つまりfの像が0になる部分空間。核[Kernel to zero]
dimV=dim(Kerf)+dim(rankA)
・平面(dimV=2)が直線(dim(Imf)=1)にうつるなら、残った次元は2-1=1が核の次元だね。
・空間が(dimV=3)が直線(dim(Imf)=1)にうつるなら、残った次元は3-1=2元が核の次元になるね。
・また、dim(V/Kerf)=dim(Imf)だから、空間の次元サイズが同じなり、V/KerfとImfは同型と言える。
(例)
R2からR2への線形写像fの表現がA= のとき、1行目の3倍を2行目にたすと、
A'=となり、rankは1だから
dim(Imf)=dim(rankA)=1(Imfは直線)
Ax=0とする。
x=(x,y)とおくと-x+2y=0でkerfは直線y=1/2で、dim(kerf)=1
(X,Y)=(-x+2y, 3x-6y) Y=-3Xだから、Imf :y=-3x。dim(Imf)=1(Imfは直線)
dimV=2=1+1=dim(Kerf)+dim(rankA)
fは2次元を1次元につぶしているから同型ではない。
V/Kerfによって、Vを直線Kerfと同じ傾きの直線の集合に分割する。
平面を直線に分類することで、
f’:1直線→1点
f’:直線をスライドする→点がスライドする
という対応関係ができるから、
f:平面→点群の準同型写像(相似)
核の割り算によって、
f’:線群→点群の同型写像(合同)
に改造できたとうことだね。
直線を移動すると、その写像f(V/Kerf)はImf上の点となり、点が移動するね。
これで、準同型写像が同型写像に整形できる。
f’:V/Kerf→imfが同型写像だ。
V/Kerf≅imfだ。
v/Kerfでimfと2つの線形空間を同型にしよう。
4.自己同型から正規部分群を作る
さっきの逆を考えてみよう。
これまでの準同型、同型は、2つの異なる領域での異なる2群の関係性がテーマだった。
こんどは1つの領域の1つの群を自分に重ねる方法、つまり、自己同型(変換)をさぐってみよう。
図形でいえば、対称図形を対称移動して自分に重ねる重ね方をさぐるようなものだね。
<内部自己同型でペアは巡回で計算できる>
「群Gの要素gで、要素xにgxg-1をする変換fをigと名付けよう。この写像igは自己合同変換だ。」
理由は、fは、f(xy)=gxyg-1=gxg-1gyg-1=f(x)g(y)だから、準同型写像。
e=f(e)-1f(e)=f(e)-1f(ee)=f(e)だから、単位元が単位元にうつるから全単射。だから自己合同だね。
そこで、この変換igをgによる内部自己同型と呼び、
y=ig(x)と移動するもとと行先のペアx,yを共役と呼ぶことにする。
xのペアyの求め方は、もちろんgxg-1を計算すればよいが、y=gxg-1の面白い方法がある。
群Gが対称群Snのとき、y=
辞書形式に書くと
x={1:x(1), 2:x(2),......, n:x(n)}, g={1:g(1), 2:g(2),......,n:g(n)}のとき、
y={g(1):g(x(1)), g(2):g(x(2)),......,g(n):g(x(n))} となる。
つまり、xのキーも値もgを作用させるだけということだ。
(例)
S3で、g=(1 2 3) , x=(1 3 2 )なら, x={1:3, 2:1, 3:2}だからgでサイクリックにxの要素がシフトして、
y={2:1, 3:2,1:3}=(1 3 2) となる。x=(1 3) ={1:3, 2:2, 3:1} なら、y={2:1, 3:3, 1:2}=(1 2)となるね。
だから、g=(1 2 3)による共役ペアは(1 3 2)→(1 3 2) , (1 3) →(1 2)のようになるね。
共役は、添字の読み替えをしているだけともいえるので、置換の型は不変だということもわかるね。
<内部自己同型のペアではみ出さないものたちが正規部分群>
・次に、gを動かしてみよう。すると変換igも動いていく。すると、共役のペアも変わると予想される。しかし、特定のかたまりは共役で閉じていることもあるだろう。
特に、群Gの部分群Nに対して、gをいろいろ変えて変換igをしても、Nに収まるとき、Nを正規部分群とする。正規部分群には、こういう定め方もある。
(Gの自己同型の集合全体をAut GとかAuto Gとかく。)
質問:S3={e,r,s,a,b,c}, N={e,r=(1 2 3),s=(1 3 2)},T={a=(2 3),b=(1 2),c=(1 3)}として、igを変化させてもNの共役がNにとどまることをコードでしらべるにはどうしたらよいでしょう。
置換で変化しない部分も形式的に統一するためにanykey関数を作り、すべてのキーの変換先を出すようにしましょう。
igx関数で、g,xから置換辞書xから共役な置換辞書yを返します。
igxs関数は、1つの置換xではなく、群の置換ぜんぶをxsで渡して、ぜんぶ共役にしたリストを返します。
make_auto関数は、群Gの部分群Hを渡すと、その全部の要素の、Gの要素gによる共役を計算したリスト
nameListを計算しながら表示します。そして、もとのHの要素の集合とnameListを蓄積したリストをユニークな集合にします。最後にそれを比較して、Hが正規部分群かどうかのメッセージを出します。
#[IN]Python==============================================================
def ami2dic(ami):
return dict(zip(ami , ami[1:] + [ami[0]]))
def amis2dics(amis):
return [dict(zip(ami , ami[1:] + [ami[0]])) for ami in amis]
# kの辞書dic_aによる行先を返す。辞書にないなら行先はk。
def ami_go(k,dic_a):
return dic_a[k] if k in dic_a.keys() else k
#あみだの辞書a,bの連結をする。
def conL(a,b):#a,bの順に演算する。
keys = list(set(list(a.keys()) + list(b.keys())))
dic ={key:ami_go(ami_go(key,a),b) for key in keys if key !=ami_go(ami_go(key,a),b)}
if len(dic)==0:
dic={1:1}
return dic
def conR(a,b):#b,aの順に演算する。
return conL(b,a)
#アミダを、(辞書,名)のタプルのリストにする。
def rotdic(S,SN):
dic=[ami2dic(x) for x in S]
return list(zip(dic,SN))
# あみだ辞書dic_aを名で返す。
def name(dic_a):
global Nlist
return [item[1] for item in Nlist if item[0]==dic_a][0]
# あみだ辞書集dicsを名のリストで返す。
def names(dics):
global Nlist
return [item[1] for item in Nlist for b in dics if item[0]==b]
# あみだ辞書の集合Hと辞書aを演算した結果リストを返す。
def Ha(H,a):
global Nlist
res=[]
for b in H:
res +=[item[1] for item in Nlist if item[0]==conR(b,a)]
return res
def aH(a,H):
global Nlist
res=[]
for b in H:
res +=[item[1] for item in Nlist if item[0]==conR(a,b)]
return res
#==================================以上が基本関数====================
#辞書リストS,名リストSNから(辞書、名)のタプルのリストにする。
def Ndic(S,SN):
return list(zip(S,SN))
def igx(g,x):
global Ssize
n = Ssize
keys=[ami_go(k,g) for k in range(1,n+1)]
vals=[ami_go(ami_go(k,x),g) for k in range(1,n+1)]
return dict(zip(keys,vals))
def igxs(g,xs):
return [igx(g,x) for x in xs]
def anykey(d):
global Ssize
n = Ssize
keys=[k for k in range(1,n+1)]
vals=[ami_go(k,d) if ami_go(k,d)!=None else k for k in range(1,n+1)]
return dict(zip(keys,vals))
#=========ここからがデータ入力
Ssize=3
e={1:1,2:2,3:3}
s=anykey(ami2dic([1,2,3]))
r=anykey(ami2dic([1,3,2]))
b=anykey(ami2dic([1,2]))
c=anykey(ami2dic([1,3]))
a=anykey(ami2dic([2,3]))
S=[e,r,s,a,b,c]
E=[e,r,s]
A=[e,a]
B=[e,b]
C=[e,c]
SN=["e","r","s","a","b","c"]
Nlist=Ndic(S,SN)
#内部自己同型の演算表を作る
def make_auto(H):
global Nlist
targetset = set(names(H))
goalList= []
G = [x[0] for x in Nlist]
print("igの対象=",names(H))
for item in G:
nameList= names(igxs(item,H))
print(name(item),"→",nameList)
goalList.extend(nameList)
goalset=set(goalList)
print(targetset,"→",goalset)
msg = f"だから、{targetset}は正規部分群"
msg += "です。" if targetset == goalset else "ではありません。"
print(msg)
return True
print("G∍gによる内部自己同型")
make_auto(E)
make_auto(A)
make_auto(B)
make_auto(C)
[OUT]====================
G∍gによる内部自己同型
igの対象= ['e', 'r', 's']
e → ['e', 'r', 's']
r → ['e', 'r', 's']
s → ['e', 'r', 's']
a → ['e', 'r', 's']
b → ['e', 'r', 's']
c → ['e', 'r', 's']
{'e', 'r', 's'} → {'e', 'r', 's'}
だから、{'e', 'r', 's'}は正規部分群です。
igの対象= ['e', 'a']
e → ['e', 'a']
r → ['e', 'b']
s → ['e', 'c']
a → ['e', 'a']
b → ['e', 'c']
c → ['e', 'b']
{'e', 'a'} → {'e', 'c', 'b', 'a'}
だから、{'e', 'a'}は正規部分群ではありません。
igの対象= ['e', 'b']
e → ['e', 'b']
r → ['e', 'c']
s → ['e', 'a']
a → ['e', 'c']
b → ['e', 'b']
c → ['e', 'a']
{'e', 'b'} → {'e', 'c', 'b', 'a'}
だから、{'e', 'b'}は正規部分群ではありません。
igの対象= ['e', 'c']
e → ['e', 'c']
r → ['e', 'a']
s → ['e', 'b']
a → ['e', 'b']
b → ['e', 'a']
c → ['e', 'c']
{'e', 'c'} → {'e', 'c', 'b', 'a'}
だから、{'e', 'c'}は正規部分群ではありません。
3.正規部分群から同型を作る
<あみだくじでも同型にする>
3本あみだG=S3={e, r=(1 2 3),s=(1 3 2), a=(2 3), b=(1 2), c=(1 3)]とするとき、
群Gを正規部分群N={e,r,s}で,NとT={a,b,c}の2つの剰余類に分割した。
すると、剰余類というマスクをかけることで、G/Nは奇数1,偶数0の加法群と同型な群になったね。
そのせいで、sN=Ns,aN=Na,......などになり
G=N+aN=N+Na=N+Tのように、Gを1つの決まった分解で表現できる。
G全体を正規部分群単位のわり算によって、きれいに分解できたわけだ。
あのガロアは、この分解のことを「固有分解」と呼んでいる。
6÷3=2個の類(コセット)。
群÷群のところの回でわかったように、
剰余類(コセット)どうしの演算を代表元を使っても群となる。これを剰余群という。
群(G,*)と正規部分群N◁Gから新しい剰余群(G/N, ★)が作れた。
これって、群の同型を作る方法になっていたんだね。
f:G/N → Z2={0 ,1}
演算:あみだの連結→剰余の加法
サイズ:ともに2
G/N≅Z2だね。
<一般化しよう>
G=S3の正規部分群NでGを割ると、G/NはNとTの固まりに分かれ、剰余群(G/N.★)
Nが0、Tが1の、2で割ったあまりの群Z2と
同型になった。これを写像fとすると、
f(N)→0になるから、N=kerf(fの核は正規部分群)ということだ。
そして、Z2=f(G)
G/N=G/Kerfだから、
G/Kerf≅f(G)
同様にして、n次交代群はn次対称群の正規部分群となるね。
G=Snの正規部分群N=AnをGで割ったG/NはNとTの類に分かれる剰余群(G/N,★)
Nが1,Tが1の2で割った余りの群Z2と同型になる。
これを写像fとするとf(N)→0でA5=Ker f だから、Sn/ An≅Z2
5.置換の型から正規部分群を作る
どんな置換の辞書も行先を出発点にしてたどり、たどり切れない出発点から同じことを繰り返すと、
巡回置換の集まりになるね。
この事実を、どんな置換も互いに素な巡回置換の積に分解できると言い表すこともできるね。
(例)
対称群S10を考えよう。
置換A=(1 2 3 4 5)(6 7 8)(1 2)と巡回置換への積分解ができるなら、置換Aの型は(5,3,2)型だという。
置換B=(2 3 4 5 6)(7 8)(1 6 9)と巡回置換への積分解ができるなら、置換Bの型も(5,3,2)型だという。
大から小へ巡回置換のサイズをならべると同じになるとき、置換Aと置換Bは同じ型と呼ぶことにしよう。
対称群Snにかぎっては、部分群Nのどの置換の型も、NとN以外にまたがることがない。
つまり、置換の「同じ型について閉じている」なら部分群Nは正規部分群だ。
(例)S3={e,r,s,a,b,c}, N={e,r=(1 2 3),s=(1 3 2)},T={a=(2 3),b=(1 2),c=(1 3)}とすると、
Nのr,sは3型、e=(1,1,1)型でこれらの型はNの中に閉じ込められているから、Nは正規部分群だ。
たとえば、P={e,a}のような群では、aの方が2型で、2型はPの外にもあるから、Pを正規部分群にすることはできないね。
++記号の演習
数学の抽象化は概念化、
つまり「用語と記号」の「約束」の世界だ。
群の「約束記号と用語」になれるために、群の性質を記号・用語で確認する演習をしたい人はどうぞ。
<準同型写像>
群Gから群G'への写像fで、演算結果の写像が写像の演算結果に等しいのが準同型写像。
「どんなx,y∈Gについてもf(x * y) =f(x)⊕f(y)とか、演算記号を略してf(xy)=f(x)f(y)」などとかける。
写像の直積f×fを使ってかくと、G上の演算*を写像P, G'上の演算⊕を写像Qとかくと、
f×f:G×G→G'×G': (x,y) →(f(x),f(y))という順序対の写像で、
演算結果の写像は、f×f(P(x,y))=f(x*y)
写像の演算結果は、Q(f×f(x,y))=Q(f(x),f(y))=f(x)⊕f(y)。この2者が等しいのが準同型写像。
・準同型写像では単位元eは単位元e'に、逆元g-1は逆元g'-1に写る。
・写像fによるGの像をim f。imfは終域G'の部分群。
<正規部分群と同型>
・x∈Gの群Nによる左剰余類と右剰余類が等しくなる(xN=Nx)ときのNが正規部分群で、
N◁Gとかく。これは前回やりました。
・群Gの部分群Nに対してすべてのgでした変換結果ig(N)がNに収まるとき、Nは正規部分群だ。
・終域の単位元e'の原像、核をK=ker f とかく。核はGの正規部分群である。
k1,k2∈Kとすると、f(k1*K2-1)=f(k1)⊕f(k2-1)=e⊕e=e'で、k1*k2-1∈Kだから、KはGの部分群。
k∈Kにg∈Gで共役作用するとig(k)=gkg-1だから、f(ig(k))=f(g)f(k)f(g-1)=e'となり、
ig(F)がFに収まるから、Fは正規部分群になる。
・ker f ={e}となるとき、GとG'は同型という。e→e'が単射だからぴったり重なるからです。G≅G’とかく。
・同型は同値関係です。自同律、反射律、推移律が成り立つからです。
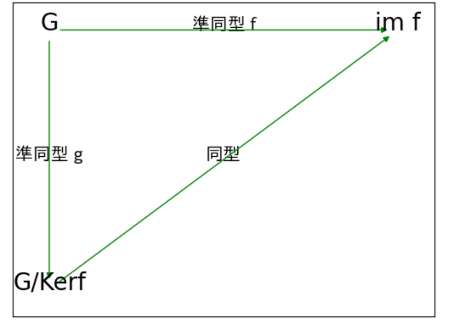
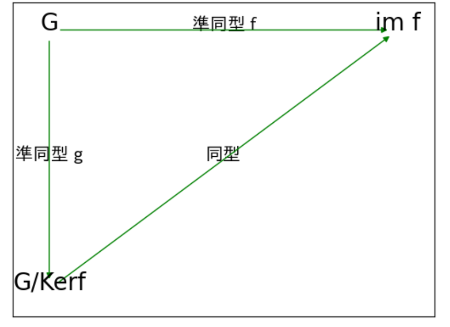
・準同型定理(第1同型定理)
準同型写像fから,fの核による商群とfの像との同型ができる。G/Ker f ≅im f
群G,G'と準同型写像f:G→G' ;x →f(x)があるとき、商群G/Ker f によって、
同型f':G/Ker f→G';x + Ker f →f(x)に加工できる。
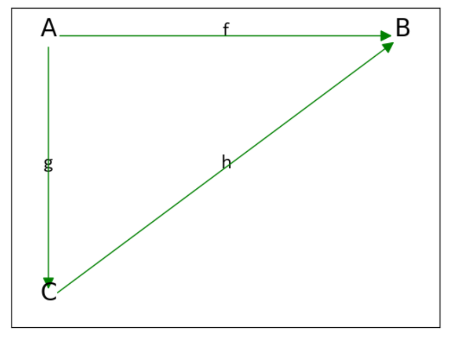
質問:可換図式としてコードで表すにはどうしたらよいでしょうか。
可換図式は、AからBにいくのに、Cを経由してA→C→Bでいけるという図式です。
道順ではなくて、写像で2通りの生き方で同じ像にいきつくというのが可換図式だね。
グラフパッケージというのは、設定を細かくしなくても見やすくレイアウトしてくれたり、レイアウトの
型を指定することで、大量のデータを視覚化できる利点があるね。
でも、少ないデータで希望のレイアウトにすることがかえって大変なこともある。
graphvizは日本語対応しているけれど、かってに、ノード位置を変えたり、線を曲線にしてしまう。
線を直線に限定することは指定で変えられるけれども、群を直角三角形に配置することが難しい。
そこで、networkxというパッケージを選ぼう。ただし、matplotlib配下で描画しているので、日本語化
を先にしなければならない。
まず、matplotlibを日本語化しましょう。
たとえば、chromebookでは、jupyter notebook上で
日本語フォントをmatplotlib用にインストールします。
[IN]
pip install japanize-matplotlib
インストールされたフォント家族の名前を表示します。
[IN]
print( plt.rcParams['font.family'] )
[OUT]
['sans-serif']から、['IPAexGothic']に変わったとしたら、
networkxでのラベル表示でこのフォント家族を指定することをお忘れなく。
辺を矢線でかきます。だから、Graphではなく、DiGraphです。
G = nx.DiGraph()
あとで、2部グラフ(bipartite_layout)に指定したレイアウト位置(pos)を取得して、あとで使います。
fが左側にかく群、nが右側にかく群です。
描画の順番の関係上、f,nのそれぞれで0番目が下に、1番目が上にくるので要注意です。
直角三角形がうまくかけないので、空の名前を使い長方形状に配置します。
そして、空のノードを消したいので、ノードの色を'white'にすることで空のノードを
消すことができるでしょう。
最後に描画する関数の引数は、グラフ構造体Gとレイアウト位置が位置の決まったpositionalパラメータ
だけど、そのあとは、自分で調べて、→の形状や色、文字の大きさをoptionalパラメータで入れてみよう。
たとえば、こんな感じだ。
nx.draw_networkx_edge_labels(G, pos,
edge_labels=labels,font_family='IPAexGothic',font_size=15,rotate = False,verticalalignment='baseline')
nx.draw_networkx(G,pos,
node_color=colorList,edge_color ='green',font_size=20,verticalalignment='baseline',arrowsize=20)
[IN]
import japanize_matplotlib
import numpy as np
from matplotlib import pyplot as plt
import networkx as nx
def kakanzushiki(f,n,funcs,E):
# グラフの作成
G = nx.DiGraph()
G.add_nodes_from(f, bipartite=0)
G.add_nodes_from(n, bipartite=1)
G.add_edges_from(E)
# グラフを描画
pos = nx.bipartite_layout(G, f)
colorList = ['white']*(len(f) + len(n))
labels = nx.get_edge_attributes(G, 'label')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels,
font_family='IPAexGothic',font_size=15,rotate = False,verticalalignment='baseline')
nx.draw_networkx(G,pos,node_color=colorList,edge_color ='green',font_size=20,
verticalalignment='baseline',arrowsize=20)
plt.show()
# グラフの設定と実行================================================================
#下におく群の名前を先にする。
f = ["A","C"]
n = ["B"]
funcs=["f", "g","h"]
f.reverse()
n=n+[""]
n.reverse()
E = [(f[1],n[1], {'label':funcs[0]}),(f[1],f[0], {'label': funcs[1]}),(f[0],n[1], {'label':funcs[2]})]
kakanzushiki(f,n,funcs,E)
一般の可換図式
準同型定理の可換図式
第1同型定理の可換図式1
第1同型定理の可換図式2
・2要素の積の集合HN={h*n|h∈HG,n∈N◁G}について、N◁HNGとなる。
h,h1,h2∈H,n,n1,n2∈N、x=h1*n1,y=h2*n2∈HNとおき、x*y-1=(h1*n1)*(h2*n2)-1=h1*n1*n2-1*h2-1=
h1*h2-1*h2*n1*n2-1*h2-1=h1*h2-1*(h2*n1*n2-1*h2-1)=h*(h2*n*h2-1)∈HN。
(カッコの中は、正規部分群に共役作用をしているのでNに収まるから。)だから、HNはGの部分群。
e∈Hだから、N∋n=ne∈HNとなり、NNHだから、NHN。
またN◁Gだから、x∈HNでNを共役なxNx-1はNに収まりNはHNの正規部分群。
<同型定理>
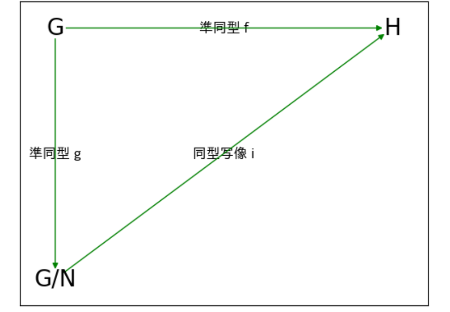
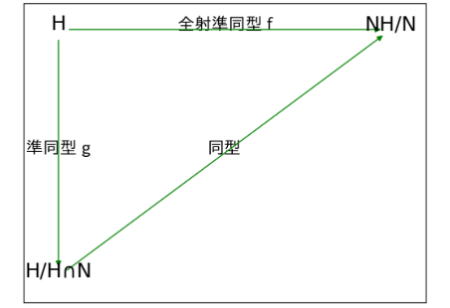
・第2同型定理
Gの部分群Hと正規部分群Nに対して、
HからHN/Nへの全単射準同型fの核は(H∩N)で、H∩NはHの正規部分群だから、HN/N≅H/(H∩N)
これを可換図式にあてはめて表示してみよう。
・HからHN/Nへの全単射準同型fの核が(H∩N)であることさえ言えれば図式から明らかだね。
x∈H∩Nは群Hの要素でもありNの要素でもあるから、
xNはNに収まるので、Nで割れば単位元に属する。つまり、f(H∩N)=e。
だから、H∩Nはfの核になる。fの核はHの正規部分群だから、fの核H∩NでHを割った剰余類と
fの像NH/Hは同型になるね。
(例)G=S4のとき、その部分群H={x|x(1)=1}≅S3に対して、N=V4={(1),(12)(34),(13)(24),(14)(23)}とする。Nの(1)以外の置換の(ab)(cd)型は、Nにすべて含まれるので、共役作用でNに収まるからNはGの正規部分群。しかも、上の定理からHN={h*n|h∈HG,n∈N◁G}について、N◁HNGとなる。
HからHN/Nへの全単射準同型fの核は(H∩N)=(1)でHの正規部分群でHN/N≅H/(1)=H=S3となる。
|N|=4, |S3|=3!=6だから、|HN|=4☓6=24=4!=|S4|となる。
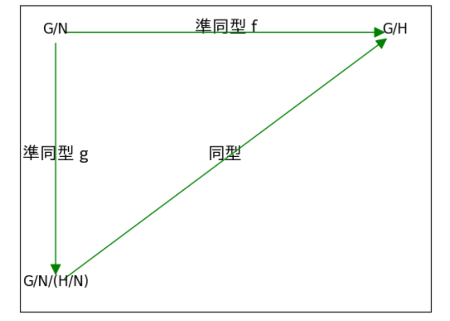
・第3同型定理
群Gの2つの正規部分群H,NでNHのときは
G/NからG/Hへの準同型写像fで、f(xN)=xHとなるものがある。
fの核はH/Nだから、核で割った剰余群(G/N)/(H/N)とG/Hは同型。つまり、G/H≅(G/N)/(H/N)
これを可換図式でかこう。
Gの要素xに対するNによる剰余類xNからHによる剰余類xHへの写像を考える。
y∈Nとすると、NHだから、y∈Hでもある。だから、xyH=xHとなるので、xNからxHへの準同型ができる。
(例)G=<x>=C8, N=C2=<x4>,H=C4=<x2>とすると、N,HはGの正規部分群で、NH。
G/H=C8/C4。(G/N)/(H/N)=(C8/C2)/(C4/C2)。だから、分数の性質みたいに同型になる。