Equazione della parabola noto il fuoco e la direttrice
Si definisce luogo geometrico l'insieme costituito da tutti e soli i punti del piano che godono di una certa proprietà, detta proprietà caratteristica del luogo.
Analogamente a quanto fatto con la carta, vogliamo costruire con Geogebra il luogo geometrico dei punti del piano equidistanti da un punto fisso e da una retta.
Per semplicità prendiamo un punto F(0,p) sull'asse y e una retta d parallela all'asse x, di equazione y = -p.
- Nella barra di inserimento scrivi:
- Prendi un punto A sulla retta d

- Traccia il segmento AF
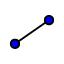
- Traccia poi l'asse del segmento AF
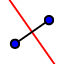
- Infine traccia la perpendicolare a d passante per A
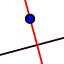
- Il punto che cerchiamo è il punto P di intersezione tra l'asse di AF e la perpendicolare a d
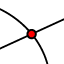
Ora rendi attiva la traccia del punto P e muovi il punto A. Cosa ottieni? Sapresti definire il luogo geometrico dei punti tracciati da P?
Con il Comando Luogo  rappresenta il luogo generato dal punto P al variare di A.
Il punto F si chiama fuoco e la retta d direttrice.
Sposta il fuoco, come varia il luogo?
Fai le tue considerazioni.
rappresenta il luogo generato dal punto P al variare di A.
Il punto F si chiama fuoco e la retta d direttrice.
Sposta il fuoco, come varia il luogo?
Fai le tue considerazioni.
Ora generalizza con carta e penna.
Se F(0,p), la retta d (direttrice) ha equazione: y = -p e il punto P che si muove sulla curva ha coordinate generiche P(x,y). Quale sarà l'equazione del luogo?
Ricorda che la proprietà del punto P è:
cioè
Che relazione c'è tra a e p?
Sapresti esprimere le coordinate del fuoco e l'equazione della direttrice in funzione di a?