Proving properties of a Perpendicular bisector
CD is the perpendicular bisector of AB.
What do you notice about the point on the perpendicular bisector? Move the point, what do you notice?
What type of triangles does the perpendicular bisector create?
Take point D and move it around. No matter where you move point D, what do you notice about the relationship between the segments DA and DB?
We can use congruent triangles to prove that these segments will always be congruent. So let's investigate the relationship between the triangles ACD and BCD by looking at some of their parts.
Using the definition of bisector, what is the relationship between the two segments AC and BC?
Using the definition of perpendicular, what is the relationship between the angles ACD and BCD?
The proof below shows the steps of what you just answered above.
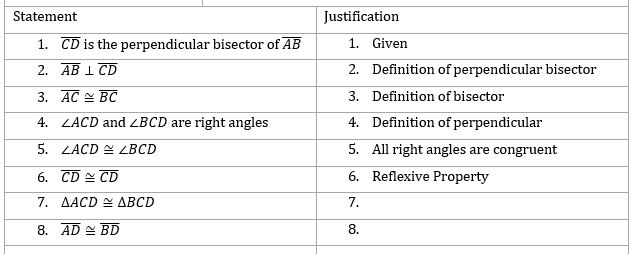
Based on the proof and what you already know, how can you say that the triangles ACD and BCD are congruent?
What should you write for the justification of step 7 in the proof?
How can you use the fact that the triangles are congruent to show that the segments are congruent? (hint: there is an important acronym!)
What should you write for the justification of step 8 in the proof?