ES 2.14
Given a line segment AB, divide it into three equal pieces (par = 6).
COSTRUZIONE:
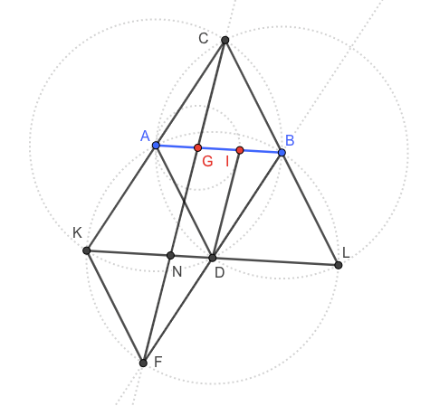
- Sia il segmento AB. Traccio la circonferenza di centro B e raggio AB.
- Traccio la circonferenza di centro A e raggio AB.
- Siano C e D i punti di intersezione delle circonferenze del punto 1 e 2. Traccio la circonferenza di centro D e raggio AB.
- Traccio la retta passante per i punti B e D. Sia F il punto di intersezione di tale retta con la circonferenza del punto 3.
- Traccio la retta passante per C e F e sia G l'intersezione di tale retta con il segmento AB.
- Traccio la circonferenza di centro G e raggio AG e trovo il punto I, intersezione di tale circonferenza con il segmento AB. Il segmento AB risulta diviso in tre parti uguali (AG, GI, IB).
- I triangoli ABC, ABD, DBL, KAD, KDF sono tutti equilateri e congruenti tra di loro per Prop I.8, dato che per costruzione i lati di tutti i triangoli sono congruenti ad AB.
- Per Prop I.32 la somma degli angoli interni di un triangolo è uguale a due angoli retti, quindi, dato che tutti gli angoli dei triangoli equilateri sono congruenti tra di loro, anche la somma degli angoli CAB + BAD + KAD è uguale a due angoli retti. Per Prop I.14 i punti K,A,C stanno su un'unica retta e quindi sono allineati. Analogamente si trova che C,B,L sono allineati, che B,D,F sono allineati e che anche K,D,L sono allineati.
- Consideriamo AB, KL e AD. Gli angoli BAD e KDA sono congruenti quindi per Prop I.27 AB // KD. Analogamente si trova che KC // FB e che AD // CL.
- Consideriamo i triangoli ACG e FND. AC FD per costruzione; gli angoli ACG e NFD sono congruenti per Prop I.29 considerando KC // FB e come trasversale FC; gli angoli CAG e FDN sono congruenti perchè lo sono i triangoli equilateri ABC e KDF. Per Prop I.26 (ASA) △ACG △FND e in particolare ND AG.
- GI AG per costruzione quindi per NC1 si ha GI ND. Essendo anche AB // KD, per Prop I.33 risulta NG // DI.
- Consideriamo i triangoli DIB e FND. DB FD per costruzione; gli angoli DBI e FDN sono congruenti perchè lo sono i triangoli equilateri ABD e KDF; gli angoli BDI e DFN sono congruenti per Prop I.29 considerando NG // DI e come trasversale FB. Per Prop I.26 (ASA) △DIB △FND e in particolare ND IB.
- Per NC1 si ottiene che ND AG GI IB e quindi in particolare che i segmenti AG, GI, IB dividono il segmento AB in tre parti uguali.