Pascal, Fibonacci, números figurados y fractales
Paseo por Manhattan
El distrito de Manhattan de Nueva York está dividido por calles paralelas y perpendiculares. Imagínate que estás en el punto azul de la siguiente imagen y quieres llegar a las casillas amarillas, verdes y azul por los caminos más cortos. Escribe, por orden alfabético, en las casillas amarillas y verdes el número de recorridos diferentes que se pueden hacer para llegar hasta ellas. Por ahora, deja la azul sin poner.
Fíjate que por ejemplo para llegar a J hay que haber llegado antes a H o a I
Ya te habrás dado cuenta de que cuanto más lejos quieras llegar, más recorridos hay. Por ejemplo, para llegar a la casilla azul hay muchas posibilidades, y sería difícil contar sin equivocarse. Nos interesaría tener un método para contar todos los caminos que llegan a cualquiera de los puntos señalados.
PREGUNTA 1
¿Has utilizado algún método para escribir los números de las casillas amarillas y verdes? Explica cómo lo has hecho.
PREGUNTA 2
Piensa en un método para escribir todos los números del triángulo del applet anterior. ¿Cómo se van poniendo los números en las filas horizontales? A partir de este triángulo, ¿cómo obtendrías los números de las casillas verdes del plano de Manhattan?
TRIÁNGULO DE PASCAL
El triángulo de números que acabas de hacer se llama TRIÁNGULO DE PASCAL, y puede seguirse indefinidamente. Este triángulo debe su nombre al filósofo y matemático Blaise Pascal (1623-1662). Sin embargo, como en muchos casos matemáticos, su origen es muy anterior. Blaise Pascal nació en Francia en 1623. Fue un niño prodigio, fascinado por las matemáticas. Cuando tenía 19 años, inventó la primera máquina calculadora que realmente funcionó. Esto era algo que otro matemático llamado Fibonacci había intentado hacer antes, pero no funcionó. Este triángulo tiene muchas curiosidades numéricas, algunas de ellas las podrás descubrir.
PREGUNTA 3
En el applet anterior, suma cada una de las filas y pon el resultado en las casillas de color beige.
¿Qué tienen de especial estos números?
PREGUNTA 4
En el applet anterior, sitúa el cuadrado azul en cualquier casilla. Fíjate en la línea azul. ¿Qué observas? ¿Cómo podríamos obtener el valor de la casilla azul de Manhattan?
PREGUNTA 5
Completa las casillas señaladas en el siguiente applet, sin necesidad de escribir todo el Triángulo de Pascal.
¿Cómo puedes obtener la casilla del hexágono azul?
¿Qué has tenido en cuenta para obtener los valores del hexágono naranja? ¿Y del amarillo?
PREGUNTA 6. Más curiosidades.
En el siguiente applet completa el Triángulo de Pascal. Suma los números que están el las líneas azules y escríbelos en las casillas grises.
Los 8 números obtenidos son el comienzo de una sucesión de números muy conocida, llamada Sucesión de Fibonacci.
Cada uno de estos números se puede obtener teniendo en cuenta los anteriores. ¿Cómo?
Escribe esta sucesión hasta el término 12º.
Puedes buscar mucha información sobre la sucesión de Fibonacci. Por ejemplo, en Wikipedia:
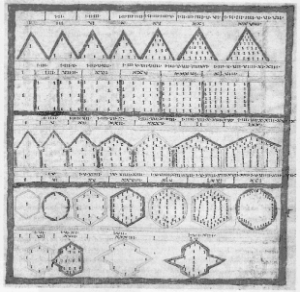
Como has podido comprobar en preguntas anteriores, se ha necesitado el poder realizar una suma de números consecutivos 1+2+3+4+5+6+7+8+9+10+11+.......... Si no son muchos, se puede realizar fácilmente, pero cuando aumenta el número de sumandos habría que tener una forma rápida de hacerlo. Como siempre en matemáticas, hay diferentes formas de poder resolverlo. Quizá conozcáis teoría de progresiones, por ejemplo. Pero vamos a plantearlo de manera geométrica, como en la antigua Grecia. En la antigüedad la Aritmética y la Geometría iban de la mano. En sus investigaciones matemáticas, Pitágoras y sus discípulos utilizaban piedrecillas (en latín calculus) o marcas que disponían según determinadas formas geométricas. Así, podían asociar números y formas, cambiar estas y observar lo que ocurría con los respectivos números, relacionar unas formas con otras, unos números con otros, etc. En definitiva, trabajaban con la forma y el número a la vez. Los resultados fueron extraordinarios y permitieron descubrir importantes teoremas y relaciones. A lo largo de la historia ilustres matemáticos como Gauss o Euler también dedicaron su tiempo al estudio de los estos números figurados. Los griegos llamaban TRIANGULARES a los números que correspondían a disposiciones de piedrecillas formando triángulos y CUADRADOS a aquellos números que se obtenían al distribuir puntos o piedrecillas de modo que la imagen obtenida fuese la de un cuadrado. Además había números rectangulares, pentagonales, hexagonales, estrellados.... En los dos applets siguientes están los siete primeros números triangulares y los siete primeros cuadrados.
PREGUNTA 7. Sobre números cuadrados
Fíjate en la imagen con puntos o la de los cuadraditos. ¿Cuál será el número cuadrado 11º? ¿Y el 12º? ¿Y el 30º?. No habrá sido necesario pintar todos los puntos, ¿cómo lo has hecho?
PREGUNTA 8. Sobre números cuadrados
Ahora observa cómo se pasa del número cuadrado 1º al 2º, del 2º al 3º,......... ¿Qué suma habría que hacer desde el 1º para obtener el 11º? ¿Cómo calcularías la suma de los 31 primeros números impares?
PREGUNTA 9. Sobre números triangulares
Fíjate en la imagen con puntos, y especialmente la del rectángulo con cuadraditos. ¿Cómo podemos calcular el número triangular 7º a partir del rectángulo? ¿Y el 12º? ¿Y el 35º? No habrá sido necesario pintar todos los puntos, ¿cómo lo has hecho?
PREGUNTA 10. Sobre números triangulares
Ahora observa cómo se pasa del número triangular 1º al 2º, del 2º al 3º, del 3º al 4º,......... ¿Qué suma habría que hacer desde el 1º para obtener el 11º? ¿Cómo calcularías la suma de los 31 primeros números naturales?
PREGUNTA 11. Sobre números triangulares
Si has sabido contestar a la pregunta 10, tienes ya un método para sumar todos los primeros números naturales que quieras. Esto te puede servir para saber cuál es el número de la casilla azul del plano de Manhattan. ¿Cuál es y cómo lo calculas?
PREGUNTA 12. Otro ejemplo para sumar los primeros números naturales
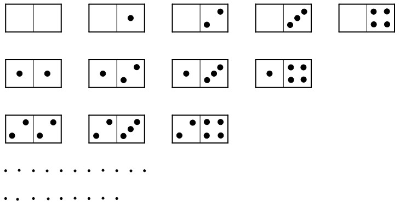
¿Cuántas fichas de DOMINÓ hay con los números 0, 1, 2, 3 y 4? Para contarlas cómodamente, se pueden poner como en la imagen siguiente. ¿Cuántas fichas de DOMINÓ hay con los números 0, 1, 2, 3, 4, 5 y 6? ¿Y con los números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9? ¿Y con las 27 letras del abecedario?
PREGUNTA 13. Números triangulares y cuadrados en el Triángulo de Pascal
En el Triángulo de Pascal, ¿dónde aparecen claramente los números triangulares? Algo más oculto en el Triángulo de Pascal, ¿cómo se obtienen los números cuadrados? Pista: fíjate en los números triangulares y haz alguna suma
En matemáticas, muchas veces necesitamos poder contar cuántos grupos diferentes se pueden hacer con unos elementos. La rama de matemáticas que estudia esto se llama COMBINATORIA La COMBINATORIA es la parte de las Matemáticas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
PREGUNTA 14. Combinatoria
Para elaborar pizzas tenemos los siguientes ingredientes: Tomate, Queso, Bacon y Jamón. Queremos hacer diferentes tipos de pizzas. ¿Cuántas diferentes se pueden hacer con 0 ingredientes? ¿Cuántas diferentes se pueden hacer con 1 ingrediente? ¿Cuántas diferentes se pueden hacer con 2 ingredientes? ¿Cuántas diferentes se pueden hacer con 3 ingredientes? ¿Cuántas diferentes se pueden hacer con 4 ingredientes?
PREGUNTA 15. Combinatoria y triángulo de Pascal
¿Dónde aparecen en el triángulo de Pascal los números obtenidos en la pregunta 14?
PREGUNTA 15. Combinatoria y triángulo de Pascal
Utilizando el Triángulo de Pascal para no tener que escribir todas Si tuviésemos 7 ingredientes para elaborar pizzas, ¿Cuántas diferentes se pueden hacer con 2 ingredientes? ¿Y con 3 ingredientes?
PREGUNTA 16. Combinatoria y triángulo de Pascal
Utilizando el Triángulo de Pascal para no tener que escribir todas las posibilidades Para hacer un equipo de baloncesto se necesitan 5 jugadores. Si hay 9 jugadores. ¿Cuántos equipos diferentes podemos formar?
PREGUNTA 17
El dibujo que te ha salido, ¿te recuerda a algo que conozcas?


PREGUNTA 18
En el Triángulo de Pascal anterior, ¿qué imagen sale si coloreas de un color los múltiplos de tres y de otro color el resto de números? ¿y si haces lo mismo con los múltiplos de cinco?