Graphをやろう
点と線でできた図をデータにしてみる。
このワークシートはMath by Codeの一部です。
<図形を使うことで処理が見やすくなる>
グラフは頂点の集まりVとそれらをいくつか結ぶ線分(辺)の集まりEでできている。
頂点がnodeか vertexかpointだ。
辺がedgeかsegmentだ。
辺の情報を与えれば、頂点の隣接状態の図としてのグラフはかける。
特に指定しなければ、点の位置は任意になる。
pythonでグラフを使うためにパッケージがいろいろ必要になる。
昔からnetworkxとかgraphvizが有名だね。
(juliaでは典型的なグラフ用パッケージがあるかどうか不明なのでpythonとnetworkでコードをかく。)
#======================
pip install scipy
pip install networkx
pip install matplotlib
#======================
import networkx as nx
G =nx.Graph()
G.add_edge(1,2)
G.add_edge(2,3)
G.add_edge(2,4)
nx.draw_networkx(G)
#======================
[OUT]
#geogebra
グラフ用のパッケージがないので、
座標Nodesをランダムに4個発生させる。
その座標を引用して、点の番号NumTを打つ。
Nodes=Sequence((RandomBetween(1,20),RandomBetween(1,20)),k,1,4)
NumT=Sequence(Text(k,Element(Nodes,k)),k,1,4)
描画のスピードは気にせず、4個の総当たりで辺のリストAllComiを作り、非表示にする。
データ作成上、リストが2層になってしまったので、辺のリストをフラットなCsにする。
AllCombi=Sequence(Sequence(Segment(Element(Nodes,i),Element(Nodes,j)),j,i+1,4),i,1,3)
Cs=Flatten(AllCombi)
ランダムに連結すると辺が3本できないおそれがあるので辺をシャッフルして前から3本選ぶ。
Take(Shuffle(Cs),1,3)
4点グラフ
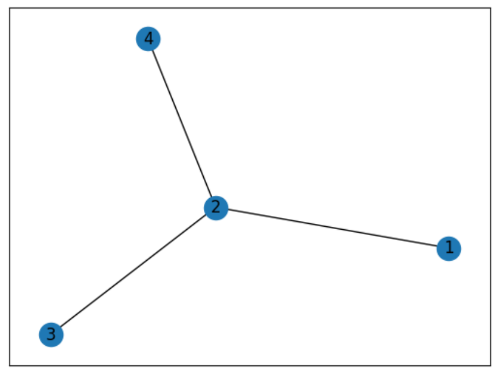
4頂点3辺グラフ
<ランダムに頂点を連結してみる>
randomにm辺できるまで、n頂点を適当に結ぶ。
辺の集合edge_setに2頂点の組を, 隣接行列graph_dataに2頂点の連結情報を1に
セットしよう。これがグラフを適当につくる関数generate_G(n,m)だ。
[IN]Python
#================================================
import random
def generate_G(n, m):
graph_data = [[0] * n for i in range(n)]
edge_set = set()
while len(edge_set) < m:
i, j = random.sample(range(n), 2)
if i > j: i, j = j, i
edge_set.add((i, j))
graph_data[i][j] = graph_data[j][i] = 1
return graph_data, edge_set
random.seed(6)
node_num = 16
edge_num = 20
figGraph, edgeSet = generate_G(node_num, edge_num)
edgeSet
figGraph
#================================================
[OUT]
{(0, 2),
(0, 4),
(0, 8),
(1, 9),
(2, 5),
(2, 7),
(2, 13),
(3, 12),
(3, 15),
(5, 11),
(5, 13),
(6, 8),
(6, 11),
(6, 13),
(7, 8),
(7, 11),
(8, 10),
(12, 13),
(12, 15),
(13, 14)}
geogebraの場合は、上記とほぼ同じでできます。
3本の頂点の選び方は、4C3=6本の辺をすべて引いてしまい。その順番をシャッフルしから前から3本
選びましたね。
これが16本になっても同じロジックで16C2=120本引いておき、その順番をシャッフルしてから20本選んだものだけを表示するという方法です。