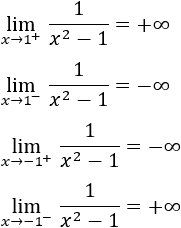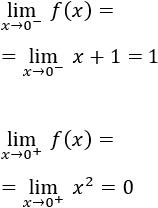Límites laterales
En esta página explicamos intuitivamente el concepto de límite lateral de una función, con ejemplos y gráficas, y proporcionamos algunos ejemplos de funciones cuyos límites laterales no coinciden.
1. Concepto de límite
Conviene recordar el concepto de límite:
Decimos que la función f(x) tiende a L cuando x tiende a a (o que el límite de f(x) en a es L ) si la función f(x) toma valores cada vez más próximos a L cuando x se aproxima al punto a.
Lo expresamos mediante
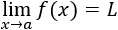 Por ejemplo, el límite de la función x2 cuando x tiende a 2 es 4:
Por ejemplo, el límite de la función x2 cuando x tiende a 2 es 4:
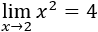 El concepto de límite lateral es el mismo, pero considerando que x se aproxima al punto a sólo por su derecha o por su izquierda.
El concepto de límite lateral es el mismo, pero considerando que x se aproxima al punto a sólo por su derecha o por su izquierda.
2. Límite lateral
El límite de f(x) por la izquierda de a es L si la función f(x) toma valores cada vez más próximos a L cuando x se aproxima al punto a por su izquierda.
Lo denotamos por
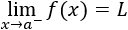 Análogamente, el límite de f(x) por la derecha de a es L si la función toma valores cada vez más próximos a L cuando x se aproxima al punto a por su derecha.
Lo denotamos por
Análogamente, el límite de f(x) por la derecha de a es L si la función toma valores cada vez más próximos a L cuando x se aproxima al punto a por su derecha.
Lo denotamos por
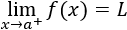 Ejemplo:
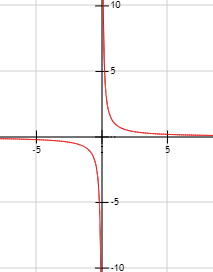
Consideremos la función f(x) = 1/x . Queremos calcular sus límites laterales en el punto x=0.
Cuando x toma valores cercanos a 0 por su derecha, f(x) toma valores positivos grandes:
Ejemplo:
Consideremos la función f(x) = 1/x . Queremos calcular sus límites laterales en el punto x=0.
Cuando x toma valores cercanos a 0 por su derecha, f(x) toma valores positivos grandes:
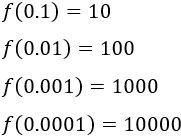 Por tanto, su límite por la derecha es infinito positivo:
Por tanto, su límite por la derecha es infinito positivo:
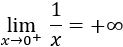 Cuando x toma valores cercanos a 0 por su izquierda, f(x) toma valores negativos pequeños:
Cuando x toma valores cercanos a 0 por su izquierda, f(x) toma valores negativos pequeños:
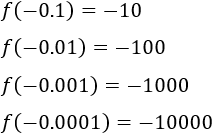 Por tanto, su límite por la izquierda es infinito negativo:
Por tanto, su límite por la izquierda es infinito negativo:
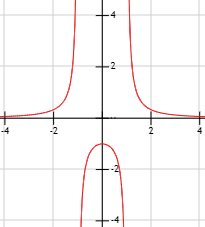
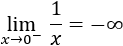 Gráfica de la función:
Gráfica de la función:
 Lógicamente, hablamos del límite de una función en un punto cuando sus límites laterales coinciden:
Lógicamente, hablamos del límite de una función en un punto cuando sus límites laterales coinciden:
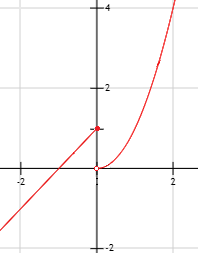
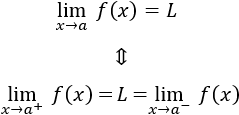 Si no es así, decimos que el límite en a no existe. Esto es lo que ocurre en el ejemplo anterior, así que
Si no es así, decimos que el límite en a no existe. Esto es lo que ocurre en el ejemplo anterior, así que
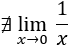
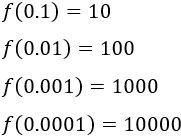 Por tanto, su límite por la derecha es infinito positivo:
Por tanto, su límite por la derecha es infinito positivo:
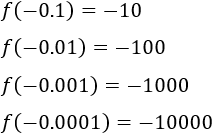 Por tanto, su límite por la izquierda es infinito negativo:
Por tanto, su límite por la izquierda es infinito negativo:
 Lógicamente, hablamos del límite de una función en un punto cuando sus límites laterales coinciden:
Lógicamente, hablamos del límite de una función en un punto cuando sus límites laterales coinciden:
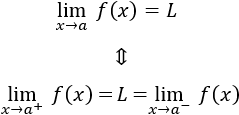 Si no es así, decimos que el límite en a no existe. Esto es lo que ocurre en el ejemplo anterior, así que
Si no es así, decimos que el límite en a no existe. Esto es lo que ocurre en el ejemplo anterior, así que