Pontok, távolságok I. (10.)
1. probléma
Adott két pont, A és B. Az AB egyenes mely P pontjára igaz, hogy
a.) PA+PB
b.)
c.)
d.)
minimális illetve maximális?
Legyen A(-1; 0), B(1; 0), P(x; 0)! Ekkor , .
a.)
Ebből következően a távolságösszeg akkor minimális, ha a P az AB szakasz pontja, ekkor a távolságösszeg az AB hosszával egyenlő, és maximum nincs.
b.)
A távolságok négyzetösszege akkor minimális, ha P az AB felezőpontja, a négyzetösszeg ekkor az AB hossza négyzetének a fele. Maximum nincs. (A négyzetes és a számtani közép közötti egyenlőtlenségből is adódik az eredmény.)
c.)
Ebből következően a távolságok szorzatának minimuma 0, a szorzat akkor minimális, ha P = A vagy P = B. A szorzatnak maximuma nincs.
d.)
,
Látható, hogy nincs minimum, és nincs maximum. (Mélyebb függvénytani ismeretekkel ez a vizsgálat pontosítható.)
2. probléma
Adott két pont, A és B. Az AB szakasz mely P pontjára igaz, hogy
a.) PA+PB
b.)
c.)
d.)
minimális illetve maximális?
Megoldás
Az 1. problémában szereplő függvényeket kell leszűkíteni a (0; 1) intervallumra.
a.) A vizsgált összeg állandó.
b.) A távolságok négyzetösszege akkor minimális, ha P az AB felezőpontja, a négyzetösszeg ekkor az AB hossza négyzetének a fele. A négyzetösszeg akkor maximális, ha P = A vagy P = B, ekkor az AB négyzete.
c.) A távolságok szorzatának minimuma 0, a szorzat akkor minimális, ha P = A vagy P = B. A szorzat akkor maximális, ha P az AB felező pontja, és ekkor az AB négyzetének a negyede. (A számtani és mértani közép közötti egyenlőtlenséggel is igazolható a kapott eredmény.)
d.) Aszámtani és a harmonikus közép közötti egyenlőtlenséggel is igazolható, hogy minimum akkor van, ha P az AB szakasz felezőpontja. Maximum nincs.
3. probléma
Adott a síkban két pont, A és B. A sík mely P pontjára igaz, hogy
a.) PA+PB
b.)
c.)
d.)
minimális illetve maximális?
Megoldás
a.) A háromszög egyenlőtlenségből következően . Egyenlőség akkor és csak akkor van, ha . Maximum nincs, hiszen az 1. problémánál már láttuk, hogy az AB egyenesen sem volt maximum.
b:)
A négyzetes és számtani közép közötti egyenlőséget valamint az a.) probléma eredményét használtuk fel. Ezekből következően egyenlőségek akkor állnak fel, ha P az AB felezőpontja. Maximum nincs, hiszen az 1. problémánál láttuk, hogy az AB egyenesen sem volt maximum.
c.) Egyenlőség (minimum) akkor és csak akkor lehet, ha valamelyik tényező 0, azaz, ha P = A vagy P = B. Maximum nincs, hiszen már az AB egyenesen sem volt.
d.) Láttuk, hogy már az AB egyenesen sem volt minimum sem maximum,így a síkon sincs.
4. probléma
Adott a egy egyenesen három pont, A, B és C , a B az A és C között van. Az egyenes mely P pontjára igaz, hogy
a.) PA+PB+PC
b.)
c.)
d.)
minimális illetve maximális?
Válasszunk olyan koordinátarendszert, melyben , a <b<c!
a.)
Nézzük a függvény grafikonját!
A kapott függvény menetének vizsgálatából látható, hogy maximum nincs, minimum van akkor, ha x = b, a minimum c – a. Akkor van minimum, ha P a középső pont, és a minimum a két szélső pont távolsága.
b.)
Teljes négyzetté alakítás után:
Ebből látszik, hogy a minimumhely (súlypont),
a minimum .
c.)
A minimum 0, a minimumhelyek: a, b, c.
c.)
Nincs szélsőérték.
5. probléma
Adott a sík egy egyenesén három pont, A,B és C , a B az A és C között van. Az sík mely P pontjára igaz, hogy
a.) PA+PB+PC
b.)
c.)
d.)
minimális illetve maximális?
a.)
A háromszög egyenlőtlenség szerint:
Adjuk össze a három egyenlőtlenséget!
Innen:
Összevetve az 4. probléma a.) részének eredményével kapjuk, hogy a távolságösszeg akkor minimális, ha P a középső pont. Maximum nincs.
Szemléltetésként
Válasszunk olyan koordinátarendszert, melyben A(a; 0), B(b; 0), C(c; 0, (a < b < c), P(x; y).
Ekkor a vizsgált távolságösszeget leíró kétváltozós függvény grafikonja:
b.)
Maximum nincs. Teljes négyzetté alakítva kapjuk, hogy a minimum A, B, C súlypontjában van.
A megfelelő kétváltozós függvény grafikonja:
c.)
. Egyenlőség (minimum) akkor van, ha P=A, P=§ vagy P=C. Maximum nincs. Távolságok szorzatát leíró kétváltozós függvény grafikonja:
Sem maximum sem minimum. A kétváltozós függvény grafikonja
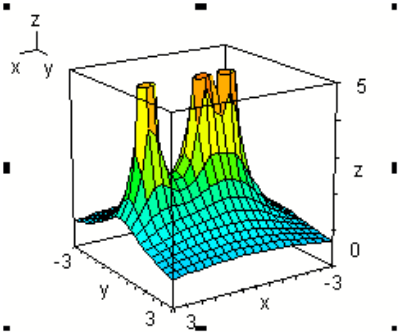
6. probléma
Adott három nem kollineáris pont, A,B és C . Az sík mely P pontjára igaz, hogy
a.) PA+PB+PC
b.)
c.)
d.)
minimális illetve maximális?
a.)
Az - talán - nyilvánvaló, hogy a távolságösszegnek nincs maximuma.
A minimumról Izogonális pont címmel itt olvashatunk.
b.)
A távolságok négyzetösszegének nincs maximuma.
Folytatás következik.