Conic Section
Cone is a surface traced out by a straight line passing through a fixed point and moving around a fixed line.
In this definition of cone,
The straight line is called generator.
The fixed point is called vertex
The fixed line is called axis
Conic section
Geometrical Approach to Conic Section
Cone लाई एउटा plane ले काट्दा बन्ने plane curve (cross section) लाई conic section भनिन्छ ।
Conic section is a plane curve obtained by section (intersection) of a cone by a plane. Based on this intersection, there are seven types of conic section. These seven types of conic section are given
below.
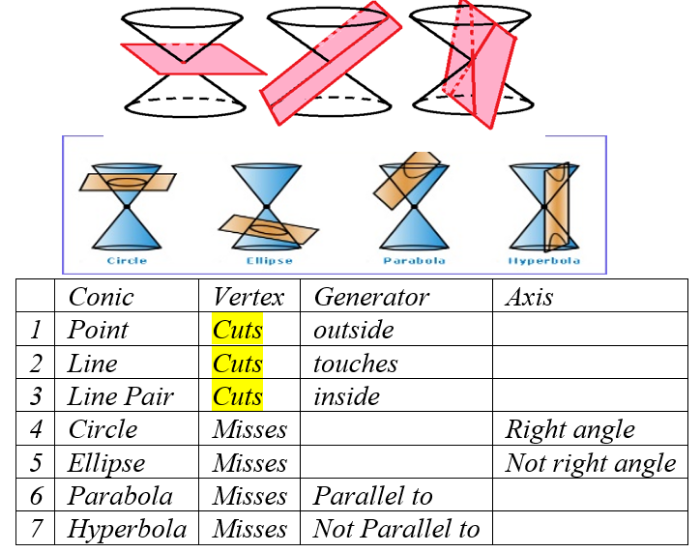
Rotation र Move slider लाई चलाएर तलको applet बाट बिभिन्न प्रकारको conic section हरु explorer गर्नुहोस
Algebraic Approach to Conic Section
In algebra, conic section can be defined with analytic expression. Therefore algebraic forms of conic section is called analytic representation.
In analytic form, Conic section can be defined from the definition of circle.
For example,
Circle is defined a locus of point whose
Distance from a fixed point = constant
The constant distance is called radius.
The fixed point is called center
====================================
Now, based on definition of circle, conic section can be defined as follows.
Conic Section is defined a locus of point whose
= constant
In this definition,
The constant ratio is called eccentricity, it is denoted by e.
The fixed point is called focus.
The fixed line is called directrix.
Based on the value of e, conic
section can be classified into three standard types. These three types are
1. Parabola (e =1)
2. Ellipse (e <1)
3. Hyperbola (e >1)
Type 1 of Conic Section (Parabola)
Parabola is a conic Section is defined a locus of point whose
e =1
The constant ratio e is equal to 1.
The fixed point is called focus.
In this parabola,
• Axis: A line perpendicular to the directrix and passing through the focus is called the "axis" of parabola
• Center: the point of intersection of parabola and axis is called center.
• Latus Rectum: A chord passing through the focus and perpendicular to the axis is called Latus Rectum.
Parabola
Type 2 of Conic section (Ellipse)
Ellipse is a conic section is defined a locus of point whose
\( \frac{\text{distance from a fixed point}}{\text{distance from a fixed line}} < 1 \)
The constant ratio is called eccentricity, where e<1.
The fixed line is called directrix, there are two such directrix
The fixed point is called focus, there are two foci
In this definition of ellipse, ellipse is the locus of point in a plane in which distance from a given fixed point (or focus) is always less than the distance from fixed line (or directrix).
Alternatively, in an ellipse, the ratio of its distance from a fixed point (focus) to its distance from a fixed straight line (directrix) is always constant and is less than 1.
Ellipse
Type 2 of Conic section (Ellipse)
Alternatively, ellipse can be defined as the locus of a point in a plane in which sum of its distances from two fixed points (or focus) is always a constant.
Ellipse 2
Type 2 of Conic section (Ellipse)
In this definition of ellipse
(a) Foci: The two fixed points of ellipse are called foci
(b) Major axis: The straight line passing through the foci is called major axis.
(c) Centre of ellipse: The middle point of the join of foci is called centre
(d) Minor axis: The straight line passing through the center and perpendicular to the major axis is called minor axis.
(e) Vertices: The meeting points of the major axis with ellipse are called vertices
(f) Length of major axis: The distance between the vertices on major axis is called length of major axis.
(g) Length of minor axis: The distance between the meeting points of minor axis with ellipse is called length of minor axis.
(i) Latus rectum: The chord passing through focus (singular of foci) and perpendicular to major axis is called latus rectum and the distance between the meeting points of latus rectum is called length of latus rectum.
Type 3 of Conic Section (Hyperbola)
Hyprobola is a conic section defined as a locus of point in which
\( \frac{\text{distance from a fixed point}}{\text{distance from a fixed line}} >1 \)
The constant ratio is called eccentricity, where e>1.
The fixed line is called directrix, there are two such directrix.
The fixed point is called focus, there are two foci.
In this definition of hyperbola, hyperbola is the locus of point in a plane in which distance from a given fixed point (or focus) is always greater than the distance from fixed line (or directrix).
Alternatively, in a hyperbola, the ratio of its distance from a fixed point (focus) to its distance from a fixed straight line (directrix) is always constant and is greater than 1.
Hyprobola
Type 3 of Conic Section (Hyperbola)
Alternatively, hyperbola can be defined as the locus of a point in a plane in which difference of its distances from two fixed points (or focus) is always a constant.
Hyprobola 2
Type 3 of Conic Section (Hyperbola)
In this definition
(a) Foci: the two fixed points in hyperbola are called foci.
(b) Directrix: the fixed straight line is called directrix.
(c) Transverse axis: the straight line passing through foci is called transverse axis.
(d) Centre: the middle point of the join of foci is called centre.
(e) Conjugate axis: the straight line passing from the centre and perpendicular to the transverse axis is called conjugate axis.
(f) Vertices: the meeting points of transverse axis with hyperbola are called vertices.
(g) Latus rectum: the straight line segment passing through focus and perpendicular to transverse axis is called latus rectum.