Euler spiral (Clothoid)
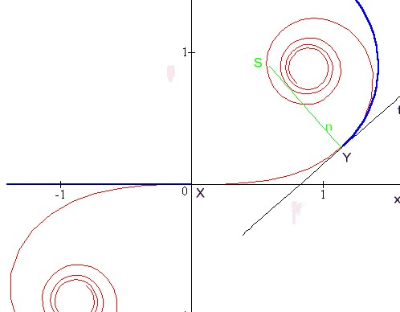
Clothoid (Euler spiral) is a curve whose curvature k changes linearly with its curve length (denote s or L).
.
Clothoids are widely used as transition curves in railroad engineering for connecting and transiting the geometry between a tangent and a circular curve. Clothoid has the desirable property that the curvature k is linearly related to the arc length L. Although its defining formulas for coordinates are transcendental functions (Fresnel integrals), the important characteristics can be derived easily from equation k = L/A2 where A2 is constant. Some applications avoid using transcendental functions by proposing polynomial approximations to the clothoid, i.e. .

Task 1
Determine the length L of Euler spiral for transition between straight road and circular arc of radius r = 9 m.
Solution: Curvature of a bend must be the same as curvature of a clothoid, i.e. and L = 16 m.
Clothoid k = L/A
Task 2
Determine an angle length α between the tangent of Euler spiral at L = 16 m and x-axis.
Solution: Formula for direction part of a clothoid.
and α = 50,92°.
Clothoid between two circumferences
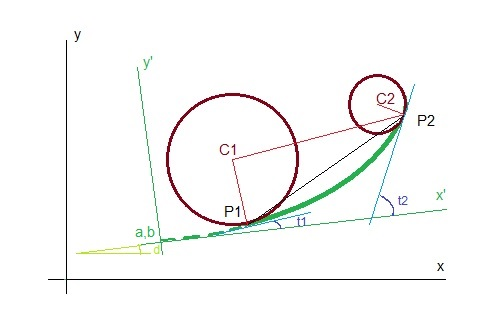
Task 3: Cubic Approximation
Replace the Euler spiral with a cubic parabola.
Solution: From the Taylor expansion of degree 3, we get an approximation of the form
.
Substituting A=15, we get the third degree algebraic transient expressed explicitly as .
Proof:

Slide 60, prezentation 07_Curves