Suma de ángulos internos de un cuadrilátero - Lección 02-01
Cuadrilátero es un polígono de cuatro lados.
Suma de los ángulos internos de un cuadrilátero: En todo cuadrilátero la suma de los ángulos internos es igual a 360°.
En el applet que se muestra a continuación los vértices del cuadrilátero son ABCD.
Los ángulos interiores del cuadrilátero son:
- Ángulo A = Ángulo DAB = Ángulo 1
- Ángulo B = Ángulo ABC = Ángulo 2
- Ángulo C = Ángulo BCD = Ángulo 3
- Ángulo D = Ángulo CDA = Ángulo 4
Actividades:
1. Active la animación del applet siguiente (botón Iniciar animación) para visualizar que la suma de los cuatro ángulos del cuadrilátro suman 360°.
La animación utiliza un solo deslizador el cual se puede manipular directamente.
Para modificar el cuadrilátero utilice los puntos A, B, C y D. El punto P es un punto libre.
Se puede mostrar las medidas de los ángulos para comprobar que su suma sea 360°.
2. Active la animación del applet siguiente (botón Iniciar animación) para visualizar que el cuadrilátero se descompone en dos triángulos.
Como se sabe, la suma de los ángulos interiores de un triángulo es 180°. Por lo tanto, la suma de los ángulos interiores de los dos triángulos que conforman el cuadrilátero equivale a 360°.
3. Sea el cuadrilátero DEFG.
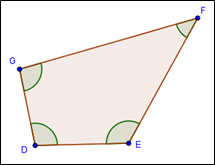
Determine la medida del ángulo D si E = 120°, F = 45° y G = 95°.
4. El cuadrilátero MNPQ es un trapecio isósceles.
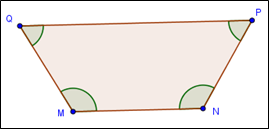
Si el ángulo M mide 120°, determine la medida de los ángulos N, P y Q.
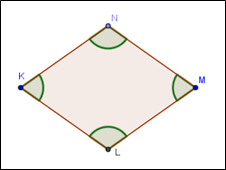
5. El cuadrilátero KLMN es un rombo.
Determine la medida de los ángulos L, M y N si el ángulo K mide 70°.