Quadrik Hauptachsentransformation Ellipsoid R³
Grundlagen
Matrixform
mit M Mittelpunkt
Beispiel:
===>
===> HAT Rotation/Drehung
===> um (1))
===>
===> HAT Translation/Verschiebung
===>
===>
Eine Quadrik xTAx+ 2aTx+a0= 0 beschreibt
- (1a)ein Ellipsoid, einen Punkt oder die leere Menge, falls alle Eigenwerte von A gleiches Vorzeichen haben
- (1b)ein Hyperboloid oder einen Doppelkegel, falls A Eigenwerte verschiedenen Vorzeichens und nicht den Eigenwert 0 hat
- (2a)ein elliptisches Paraboloid, einen elliptischen Zylinder, eine Gerade oder die leere Menge, falls A den Eigenwert 0 hat und die anderen beiden gleiches Vorzeichen haben
- (2b)ein hyperbolisches Paraboloid, einen hyperbolischen Zylinder oder zwei sich schneidende Ebenen, falls A den Eigenwert 0 hat und die anderen verschiedenes Vorzeichen haben
- (3)einen parabolischen Zylinder, eine oder zwei parallele Ebenen, oder die leere Menge, falls A den doppelten Eigenwert 0 hat.
Fallbeispiel entnommen Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD
Die Inputbox liefert die Gleichung in der AlgebraView aus. Das führt zur Rundung von Werten (z.B.) was zum Teil dramatische Auswirkungen durch Rundungsfehler haben kann. Ein exakte Rechnung erhalten sie, wenn sie die Gleichung im CAS Zeile 3 eingeben ===> q0:=
5: C Koeffizienten der Quadrik
6: Koeffizientenmatrix A (quadratische x² und gemischte xy)
7: Vektor a der x,y,z Koeffizienten für Matrixgleichung
8: Konstante a0
10: Kontrolle Ausgangsgleichung qA = (x,y,z) A (x,y,z) + a (x,y,z)=a_0
11: Diagonalisierung JordanDiagonalisation
JD(1) Drehmatrix ===> Rn (muss noch normalisiert werden),
JD(2) Matrix der Eigenwerte ===> D
12: Drehmatrix R - normalisieren JD(1)
13: Determinante R
Check Drehmatrix det(R)=1 ===> Col Change [Spalte für Korrektur*(-1)]
Ausrichten der Reihenfolge der Eigenwerte/Eigenvektoren ===> EV xchg [{1,2,3}]
durch Zeilen/Spalten-Tauschmatrizen TxR bzw. TxEV
14: Koeffizientenmatrix D der gedrehten Quadrik qD
16: Gleichung achsenparallele Lage - Drehung - qD: (x,y,z) D (x,y,z) + a R (x,y,z) = a_0
17: QE Koeffizienten für quadratische Ergänzung
19: Mq Ursprung des KO für qD und Verschiebevektor in Ursprung (0,0,0)
20: T (Translate) zum Einsetzen in qD für Verschiebung in KO-Ursprung.
21: qN transformierte Quadrik
22...===>Achsengeraden qA: gax, gay, MA Ursprung gedrehte Form qD, Drehwinkel , Drehachse gD
Quadratisches Ergänzen
HAT-Abbildung
Beispiele (Gleichung immer mit Konstante auf rechter Seite eingeben)
x² + 2y² + 3z² + 2x y + 2x z + 2y z + x = 1
2x² + y² + z² + 2x y + 2x z + 2y z + x = 1
3x² + 5y² + 3z² + 2x y + 3x z + 3y z + 8x = 5*
7x² + 7y² + 4z² - 4x y - 2x z - 2y z - 70x + 38y + 28z = -202
5x² - 10x y - 4x z - 40x + 5y² + 4y z + 52y + 8z² + 64z = -164
1 / 4 x² + 4y² + (z - 3)² = 1 (Schönheitspreis: EV xchg [1,3,2] Col Change [3])
 H(ochkant) Version fürs Smartphone
H(ochkant) Version fürs Smartphone
 vgl. Arndt Brünner
[Online und Touch Versionen rechnen oft unvollständig oder fehlerhaft - komplexe Quadriken benötigen ausgiebige Rechenzeiten]
- lokal installierte Apps: ggb5(win) arbeitet stabil - ggb6 win mit Einschränkungen stabil -
vgl. Arndt Brünner
[Online und Touch Versionen rechnen oft unvollständig oder fehlerhaft - komplexe Quadriken benötigen ausgiebige Rechenzeiten]
- lokal installierte Apps: ggb5(win) arbeitet stabil - ggb6 win mit Einschränkungen stabil -
| ==> ==> ==> |
 H(ochkant) Version fürs Smartphone
H(ochkant) Version fürs Smartphone
 vgl. Arndt Brünner
[Online und Touch Versionen rechnen oft unvollständig oder fehlerhaft - komplexe Quadriken benötigen ausgiebige Rechenzeiten]
- lokal installierte Apps: ggb5(win) arbeitet stabil - ggb6 win mit Einschränkungen stabil -
vgl. Arndt Brünner
[Online und Touch Versionen rechnen oft unvollständig oder fehlerhaft - komplexe Quadriken benötigen ausgiebige Rechenzeiten]
- lokal installierte Apps: ggb5(win) arbeitet stabil - ggb6 win mit Einschränkungen stabil - HAT-EllipsoidR3_EVX2.ggb
HAT Reihenfolge Eigenwerte 600,030,009 EV xchg [{3,1,2}] - Col change [3]
![HAT Reihenfolge Eigenwerte 600,030,009 EV xchg [{3,1,2}] - Col change [3]](https://beta.geogebra.org/resource/eywf9aka/XrtRFQbNHg6u7V4P/material-eywf9aka.gif)
Mögliche Lage der Hauptachsen
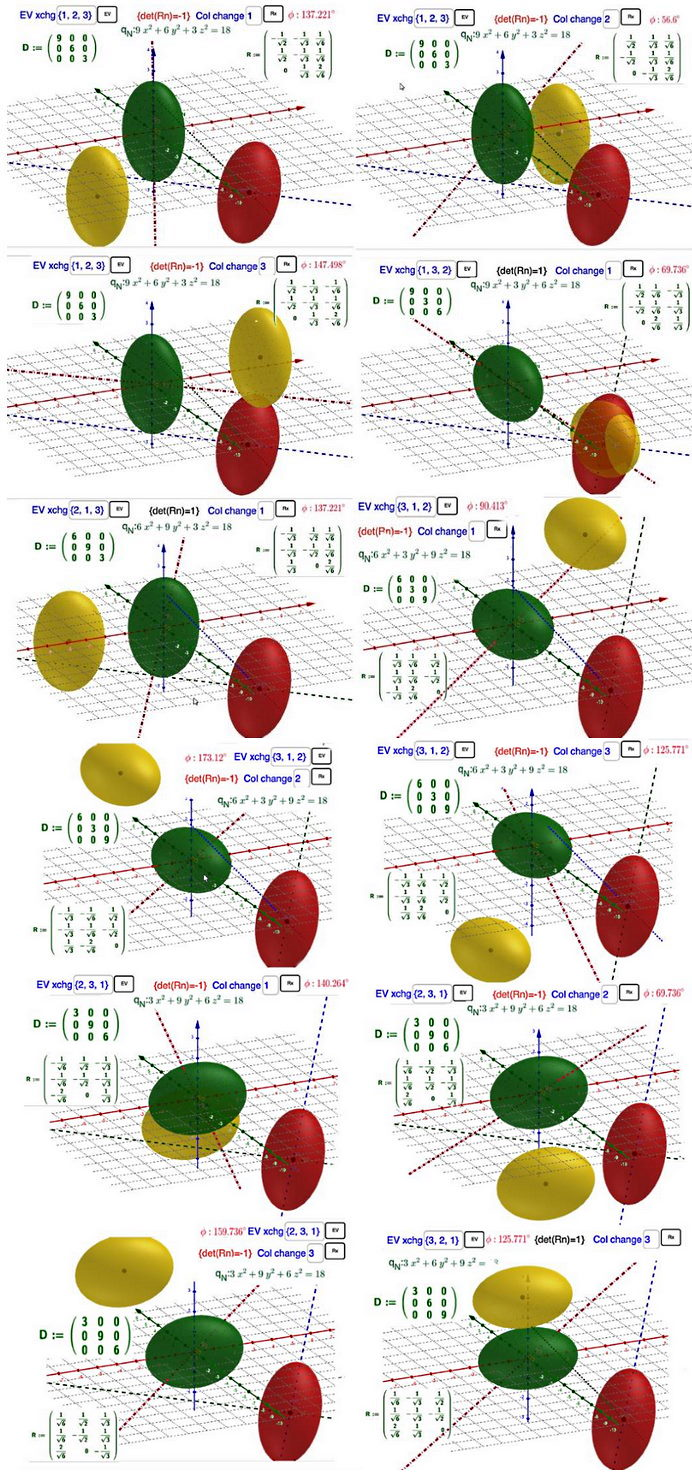
Anwendung
Entwicklungshistorie und technische Hinweise
Im Aufbau