Curves of constructive and destructive interference from two point sources. Condition for the angles at which these curves are observed in the "far" interference field
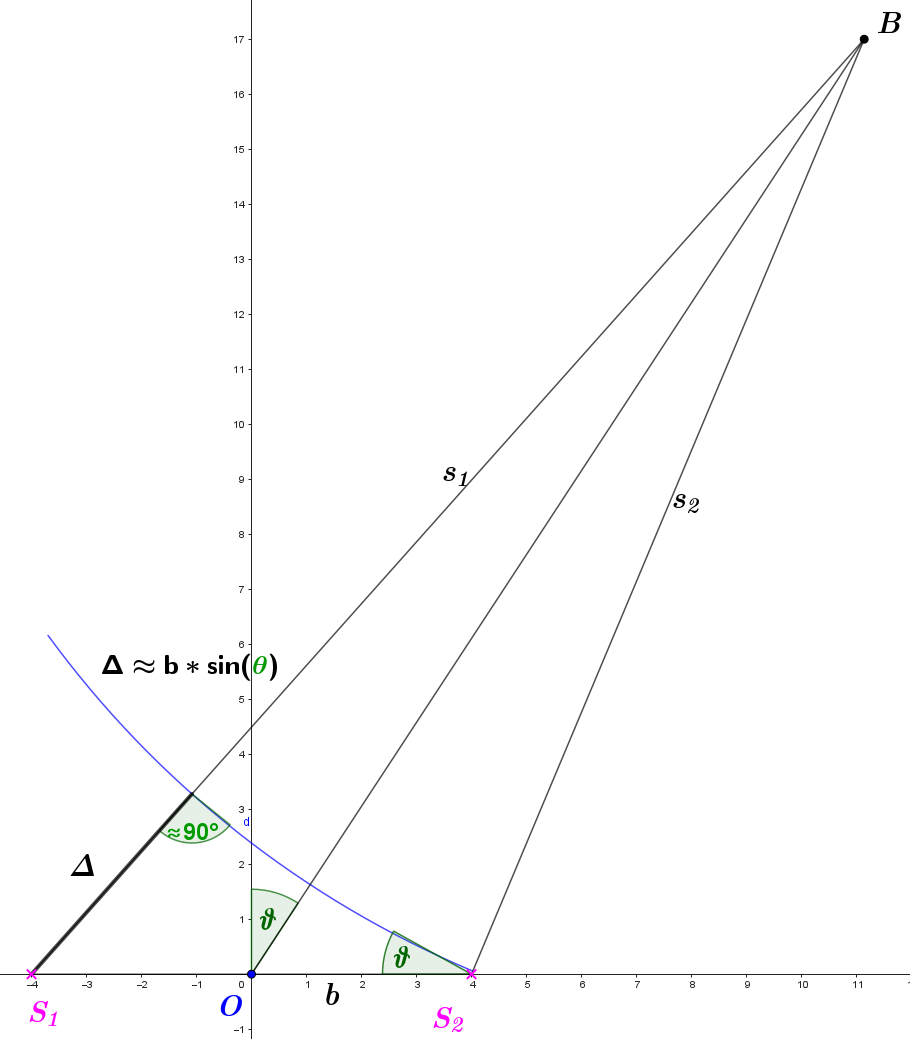
Here we consider the case of far field interference. In this region, the angular position of constructive and destructive interference is determined by the formula b*sin(θ)=r*λ, where r=-⌊b/λ⌋,..., 0, ..., ⌊b/λ⌋ with step=0.5. The applet contains a derivation of this formula using the limit transition, and below the applet in the figure there is a derivation of the same formula based on known geometric representations..
To study this phenomenon, I suggest the following exercises:
By varying the r-values and following the interference lines, one can observe changes in the angular position of the maxima and minima of the line intensity. Three methods are given for calculating the x-coordinates of the corresponding positions of the extremes of the oscillation intensity:
- x(D), where point D is the intersection of the hyperbola with the line u of the observation screen,
- the result of replacing the hyperbola in the far field by its asymptote,
and
- a calculation that is valid in the approximation of small angles of observation - this formula is usually given in the literature.
Compare the results and draw conclusions about the conditions of applicability of the given calculation formulas.
All these measurements can be made by varying
- the ratio of the distance b between the sources to the wavelength λ: b/λ,
- the distance L between the sources and the screen.
The previous applet considers the case of near-field interference.
Far interference field of two coherent radiation sources
Conditions for observing constructive or destructive interference in the "far field" at point B: Δ= r*λ or Δ = (r+ ½)*λ, r = 0 , ± 1 , ± 2 , ± 3 …
P.S. Very useful demo applet "Interference from Two Sources".