Method of Lagrange multipliers. Relative positioning of repulsive movable points on a circle.
Let L be a circle of radius R around the point O: L:={x∈ℝ2: ||x||=R}. There is a set lP={p1, p2,...,pn} of n movable points and with each pi∈L,{(xi,yi)∈L:i = 1,...,n} -their coordinates. Let the points be "repulsive".
Problem: use the method of Lagrange multipliers to find distribution of "repulsive" points on a circle corresponding to the maximum of their sum of mutual distances.
This means need to find out such mutual arrangement of "repulsive" set of particles on a circle, when each point of this set is GM of the remaining n-1 points. We assume that the equilibrium - stationary state in system of "charges" is reached if the sum of their mutual distances is maximal. Iterative approach of particle placement is applied for achieving a stationary state.
Iterative methods for optimization
There is a system of equations: ∇f(x,y)= λ*∇g(x,y). A local optimum occurs when ∇f(x,y) and ∇g(x,y) are parallel, and so ∇f is some multiple of ∇g. I propose iterative procedures in which each step produces is a more accurate approximation finds the Maximal Distance Sum.
Relationship between vectors of two consecutive iterations is defined by . This is the new position of point ps∈L. All points are successively corrected (s = 1,2, ..., n) until the system of points comes to a stationary state. Finally, at the end of iterations they must match: ps=ps* for all s=1,2,...,n. The number of correction steps is carried out until the center of mass of n particles from lP (with a certain degree of accuracy) will not be in the center of the circle.
The solution of the above Lagrange problem means that in" equilibrium " the positional vectors ∇gs:=, for each point from lP and the sum of the unit vectors other n-1 points ∇fs:=must be parallel. For a similar problem of the Maximum squares Distance Sum the gradients are ∇fq s:=.
Initial, intermediate and final-the" equilibrium " location of points on the circle as a result of an iterative procedure leading to the Maximum Distance Sum condition.
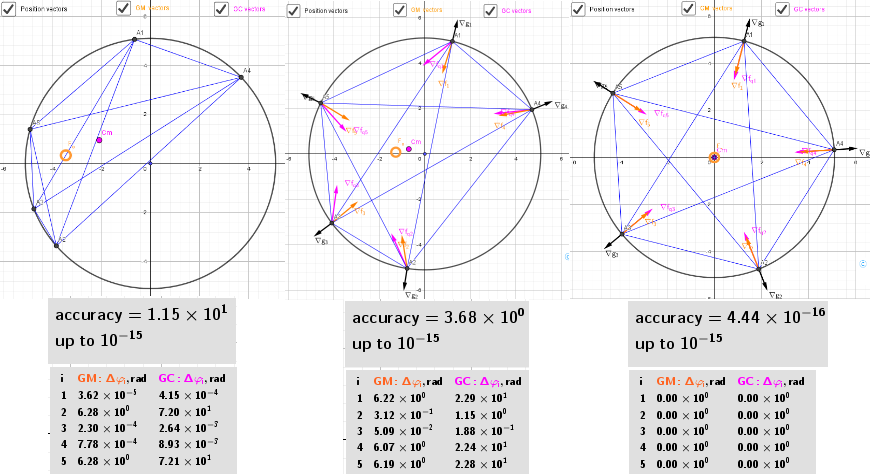
Some results
-Points are distributed evenly on the circle
-It can be seen from table that in the "equilibrium" state is achieved not only the Maximal Distance Sum but also the Maximum squares Distance Sum. This means that each point on the circle is both the geometric median and the geometric center of the other remaining points.
Main iteration formulas in applet
Execute( Join(Sequence(Sequence("SetValue(A"+i+",(0,0)+R UnitVector( CopyFreeObject[Sum[Zip[UnitVector(A"+i+"-lP(r)),r,Sequence[n]\{"+i+"} ]]] ))",i,1,n),ii,1,i0) ) )
SetValue[Wi_P,Sequence[ Sum[Zip(UnitVector(a-lP(i)), a, lP \ {lP(i)}) ],i,1,n] ]
SetValue[Wi_Pc,Sequence[Sum(lP \ {lP(i)}) / n,i,1,n] ]
SetValue[Wii_P,Sequence[Angle[Vector[lP(i)], -Vector[Wi_P(i)] ],i,1,n] ]
SetValue[Wii_Pc,Sequence[Angle[Vector[lP(i)], -Vector[Wi_Pc(i)] ],i,1,n] ]
lVectorGM = Zip(Vector(a, a + 1.5UnitVector(b)), a, lP, Vector(b), Wi_P)
lVectorGC = Zip(Vector(a, a + 1.5UnitVector(b)), a, lP, b, Wi_Pc)
lVectorP = Zip(Vector(x0, x0 + UnitVector(x0)), x0, lP)
Applets in a book:
Description. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Applet. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Finding the location of geometric medians on the circle of discrete sample points depending on the position of the test point.
Method of Lagrange multipliers. Relative positioning of repulsive movable points on a circle.
Generating an extreme arrangements of points on a circle
Generating an extreme arrangements of points on a sphere
Generating an extreme arrangements of points on a sphere with more structured calculation program-GeoGebra Forum-
https://help.geogebra.org/topic/geogebra-windows-portable-zip-for-december