Teorema
L'asse di un segmento è il luogo dei punti del piano equidistanti dagli estremi del segmento.
In base alla definizione di luogo geometrico, per dimostrare questo teorema, si devono dimostrare due proposizioni diverse:
- tutti i punti appartenenti all'asse (retta perpendicolare passante per il punto medio del segmento) sono equidistanti dagli estremi del segmento;
- tutti i punti del piano equidistanti dagli estremi del segmento appartengono all'asse.
Dimostrazione 1
Ipotesi: P appartiene all'asse di AB
Tesi:
Dim:
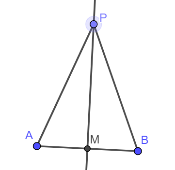
| I due triangoli AMP e BMP sono congruenti per il 1° criterio di congruenza, dato che: gli angoli AMP e BMP sono con congruenti perchè retti, perchè M è il punto medio di AB, PM è in comune. Pertanto, perchè elementi corrispondenti in triangoli congruenti. | |
Dimostrazione 2
Ipotesi:
Tesi: P appartiene all'asse di AB
Dim:
Il triangolo APB è isoscele sulla base AB perchè i lati AP e PB sono congruenti per ipotesi. Pertanto, la mediana PM è anche altezza. Possiamo dedurre che PM è l'asse del segmento perchè è perpendicolare al segmento (in quanto altezza) e passa per il suo punto medio (in quanto mediana).
Quindi, P appartiene all'asse del segmento di AB.