Coorindinacantional Figures and their Areas
Drills
These are drawings of three-dimensional objects. Which one doesn’t belong? Explain your reasoning.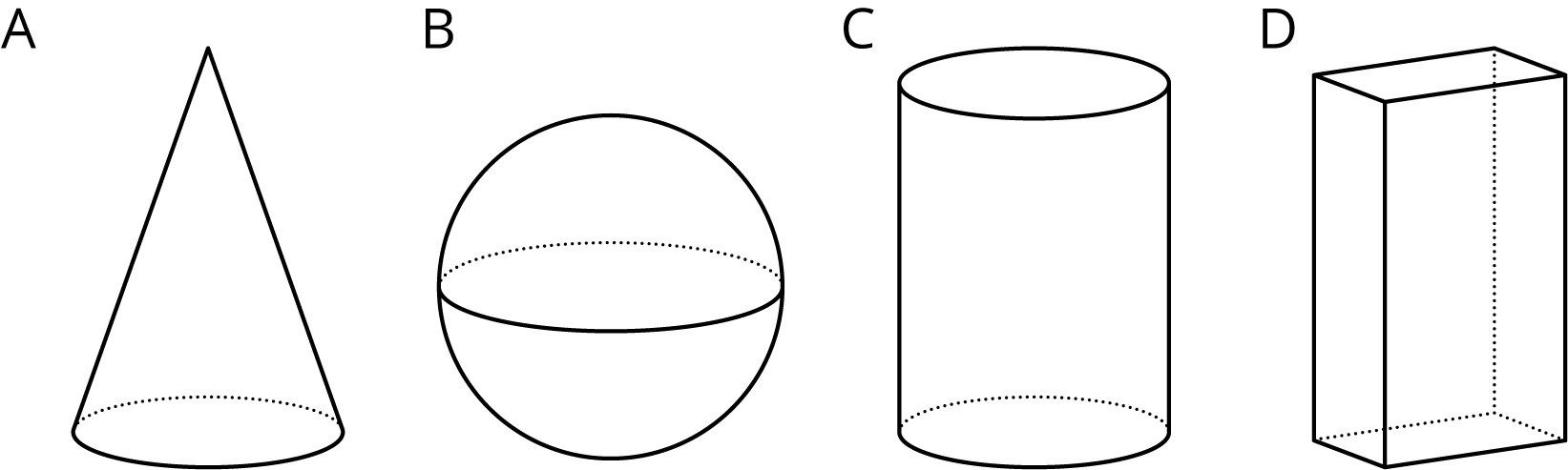
Teacher Diagram/Objective
ACTIVITY: 20 minutes11.2: Height and VolumeCCSS Standards: AddressingCCSS Standards: Building towardsIn this activity, students investigate how the height of water in a graduated cylinder is a function of the volume of water in the graduated cylinder. Students make predictions about how the graph will look and then test their prediction by filling the graduated cylinder with different amounts of water, gathering and graphing the data (MP4).LaunchArrange students in groups of 3–4. Be sure students know how to measure using a graduated cylinder. If needed, display a graduated cylinder filled to a specific measurement for all to see and demonstrate to students how to read the measurement. Give each group access to a graduated cylinder and water.Give groups 8–10 minutes to work on the task, follow with a whole-class discussion.For classrooms with access to the digital materials or those with no access to graduated cylinders, an applet is included here. Physical measurement tools and an active lab experience are preferred.
Use the applet to investigate the height of water in the cylinder as a function of the water volume. Before you get started, make a prediction about the shape of the graph. Check Reset and set the radius and height of the graduated cylinder to values yo
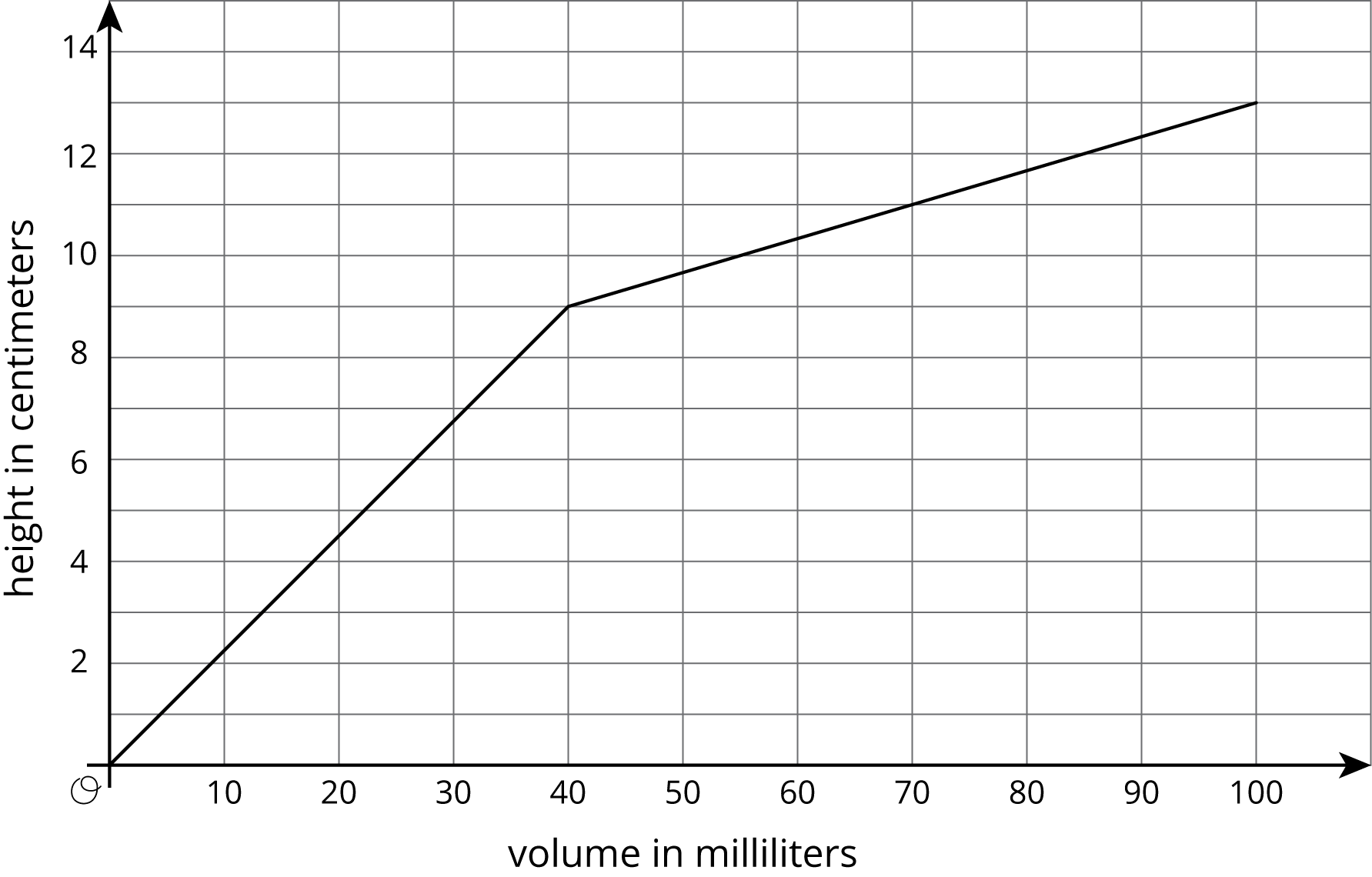
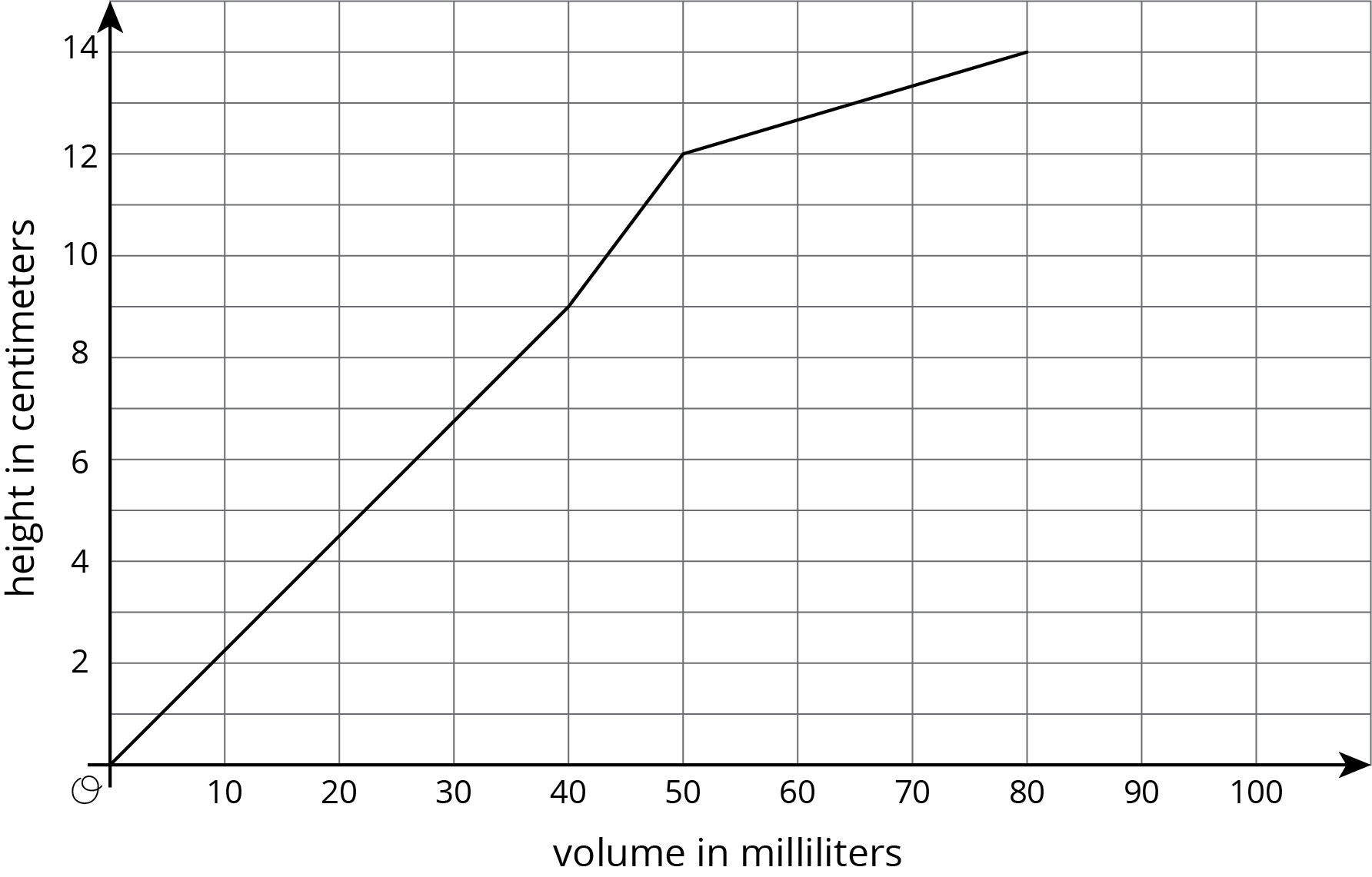
Using the points below do this; Create a graph that shows the height of the water in the cylinder as a function of the water volume. Choose a point on the graph and explain its meaning in the context of the situation.
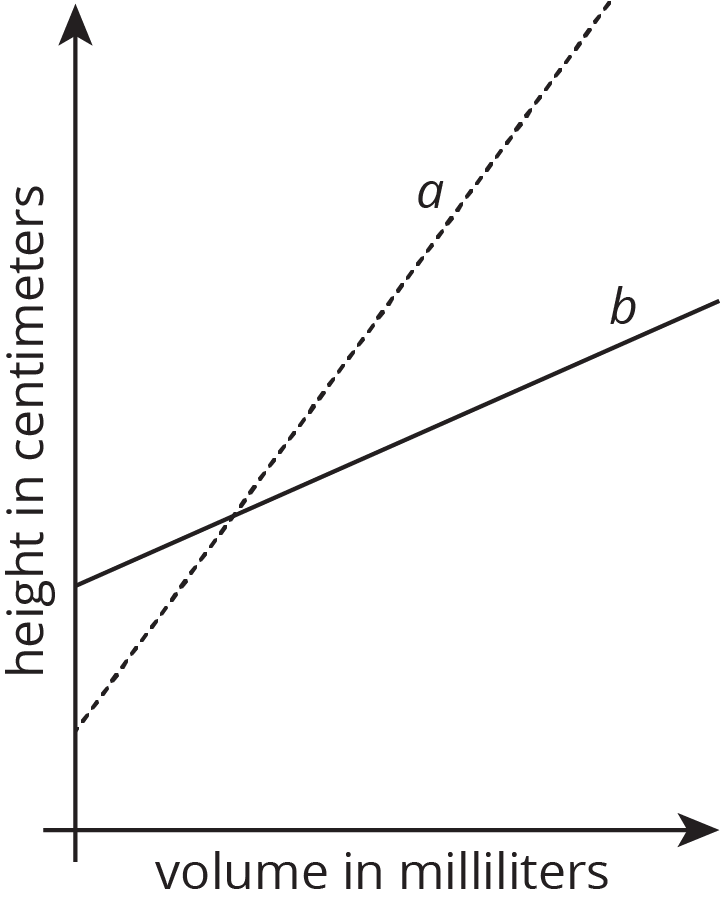
Student-Facing Task StatementTwo cylinders, a and b, each started with different amounts of water. The graph shows how the height of the water changed as the volume of water increased in each cylinder. Which cylinder has the larger radius? Explain how you know.